Riassunto / Abstract

L’esperienza consiste nel verificare la relazione che esprime l’energia potenziale elastica di una molla in funzione del suo allungamento; l’analisi del moto oscillatorio lungo la verticale viene eseguita utilizzando il concetto di energia potenziale e più in generale il concetto di conservazione dell’energia meccanica. La strumentazione necessaria per condurre l’esperimento è colloca l’esperienza nella categoria del laboratorio povero. 

Scheda sintetica delle attività

Dopo essersi procurati almeno due molle, si misurano le loro costanti elastiche e si prende nota della loro lunghezza a riposo. Successivamente si fissa un estremo di una delle molle a una massa e l’altro estremo a un supporto fisso (per esempio il tavolo del laboratorio) avendo cura che la molla e la massa siano disposta lungo la verticale.
Si lascia cadere la massa dalla posizione di molla a riposo e si misura l’altezza da terra (o dal tavolo) della massa nel momento della massima elongazione della molla, verificando la relazione che descrive l’energia potenziale della molla in funzione del suo allungamento. 
L’esperienza viene ripetuta con più masse osservando la relazione di proporzionalità tra la massa utilizzata e il quadrato degli allungamenti prodotti. 

Risorse necessarie

• Alcune molle con costante elastica nota o misurata;
• set di masse da laboratorio;
• metro flessibile;
• una fotocamera, anche di uno smartphone, per misurare con maggior precisione gli allungamenti massimi (opzionale).

Prerequisiti necessari

• Il principio di conservazione dell’energia meccanica;
• il concetto di energia potenziale;
• l’espressione dell’energia potenziale per la forza peso.

Obiettivi di apprendimento

Acquisire i concetti fondamentali di energia e conservazione della stessa per via sperimentale.

Dotazioni di sicurezza

Nessuna

Svolgimento

Si dispone la molla in posizione verticale con un estremo fissato al banco di lavoro e l’altro alla massa di prova;  si controlla che la massa sia ferma e che la molla sia nella sua posizione di riposo (ci si può eventualmente aiutare legando i due estremi della molla con un filo sottile da tagliare nel momento in cui si inizia la presa dati).
Parallelamente alla molla si posiziona un metro a nastro che sarà necessario per misurare la posizione della massa di prova. Successivamente si rimuove il vincolo che tiene inizialmente ferma la massa e si osservano le oscillazioni da essa compiute, leggendo sul metro a nastro la posizione di massima elongazione della molla. In questa fase può essere utile riprendere le oscillazioni con uno smartphone al fine di poter valutare meglio la minima distanza dal suolo raggiunta dalla massa. 
Nella posizione iniziale la massa possiede solo una energia potenziale gravitazionale \(E_{pi} = m g h_i\) dove \(h_i\) rappresenta la distanza iniziale dal suolo; l’energia potenziale elastica è nulla poiché la molla si trova a riposo. 
Quando la massa tocca la quota minima avrà velocità nulla e quindi energia cinetica pari a zero; per il teorema di conservazione dell’energia meccanica possiamo assumere che tutta l’energia potenziale iniziale si sia trasformata in energia potenziale elastica, cioè:

\[m g h_i = m g h_f + E_{el} \rightarrow E_{el} = m g (h_i-h_f) = m g \Delta h\]

Dopo aver misurato diversi valori per l’energia potenziale elastica in funzione di \(\Delta h\) possiamo procedere a verificare la relazione \(E_{el} = \frac{1}{2} K ( \Delta h)^2\) [1] compiendo una regressione lineare tra le quantità \(E_{el}\) e \(( \Delta h)^2\).

Raccolta ed elaborazione dati molla n.1
La tabella 1 e la figura 1  riportano i valori sperimentali ottenuti nel caso di una molla con valore di \(k = 14,7 N/m\); la distanza della massa dal suolo nelle condizioni iniziali è di 47.7 cm.

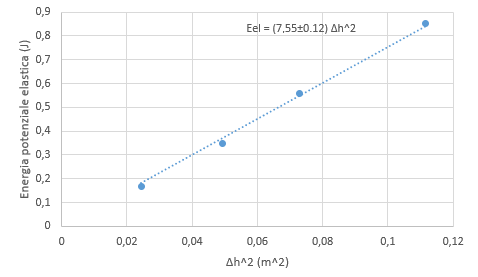
Dalla regressione lineare si ottiene un valore per il coefficiente angolare (che fisicamente corrisponde a \(\frac{1}{2}k\)) di \((7.55 \pm 0.12) N/m\) da cui ricaviamo un valore di \(k= (15.1 \pm 0.24) N/m\) in accordo entro \(2\sigma\) con il valore nominale.

Raccolta ed elaborazione dati molla n.2
La tabella 2 e la figura 2  riportano i valori sperimentali ottenuti nel caso di una molla con valore di k = 31.9 N/m; la distanza della massa dal suolo nelle condizioni iniziali è di 49,2 cm.

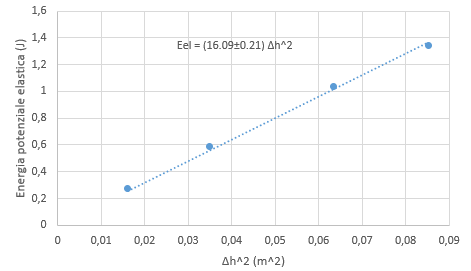
In questo secondo caso si ottiene dalla regressione lineare un valore di \(k= (32.18 \pm 0.42) N/m\) in pieno accordo con il valore nominale della costante elastica della molla n.2.

La difficoltà maggiore dell’esperimento è nella lettura della minima distanza da terra della massa oscillante e per tale ragione si consiglia l’uso di uno smartphone ed uno dei tanti software free che permettono di esaminare il filmato al rallentatore. 

Autori

Pierri Raffaele

Specifiche esperimento Materia Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano Materiale specifico Molle di costante nota, masse di prova, metro flessibile Durata esperimento in classe 1 h Capacità di bricolage/assemblaggio Sì Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati No Necessità di uno smartphone No Parole chiave Meccanica Dinamica del punto materiale Energia Energia potenziale