Riassunto / Abstract

L’esperimento propone la realizzazione di una “bilancia inerziale” per la misura della resistenza che un corpo oppone a cambiare il suo stato di moto quando è soggetto ad una forza, cioè della massa inerziale di un corpo. Dopo una opportuna taratura della bilancia, viene mostrato come utilizzare la bilancia e la sua retta di taratura per la misura della massa inerziale.
Viene poi illustrata la metodologia sperimentale da seguire per confrontare i valori della massa inerziale e della massa gravitazionale, quest’ultimi misurati con una comune bilancia.

Scheda sintetica delle attività

Lo scopo dell’attività è quello mettere in grado lo studente di caratterizzare la massa inerziale come una proprietà dinamica e di fornire uno strumento per la sua misura.

Ogni corpo mostra una resistenza, una inerzia a mettersi in moto se in quiete e ad arrestarsi se in movimento.
Per questa proprietà, tipica di ogni corpo, si usa in fisica il nome di massa inerziale.
Una definizione operativa della massa inerziale deve far riferimento a qualche proprietà misurabile dei sistemi dinamici che dipende da essa.
In questa esperienza ci si propone di misurare tale grandezza attraverso la misura del periodo delle oscillazioni di un corpo soggetto ad una forza elastica. 

Risorse necessarie

• Due vassoi di metallo;
• nastri elastici rigidi in acciaio di circa 35 cm;
• morsetti di montaggio;
• viti e bulloni per assemblaggio;
• set di oggetti identici (ad esempio pesiera);
• fotocamera o cronometro.

Prerequisiti necessari

• Moto armonico;
• nozioni di teoria degli errori;
• saper utilizzare un foglio di calcolo;
• saper interpolare dati sperimentali.

Obiettivi di apprendimento

• Acquisire il concetto di massa inerziale;
• saper applicare il modello matematico che descrive il moto armonico alle piccole oscillazioni;
• distinguere i concetti di massa inerziale e di massa gravitazionale.

Dotazioni di sicurezza

Nessuna

Svolgimento

Taratura della Bilancia
L’oggetto mostrato in figura 1 per piccoli spostamenti orizzontali si comporta come un oscillatore armonico. Esso sarà d’ora in avanti chiamato “bilancia inerziale” poiché attraverso la misura del suo periodo di oscillazione è possibile ricavare il valore della massa inerziale del corpo che si muove di moto armonico.

Come tutti gli strumenti di misura, la bilancia inerziale proposta deve consentire di confrontare la massa inerziale di un corpo qualunque con quella di un campione di riferimento che costituisce l’unità di misura. 

Per iniziare sarà necessario procurarsi un insieme di oggetti uguali che rappresenteranno le copie del campione dell’unità di misura scelta per la massa inerziale (ad esempio i pesi di una pesiera).

Lo scopo della prima misura è verificare che tutti i pesi campione abbiano lo stesso periodo di oscillazione \(T\) (entro le incertezze legate alla misura) e quindi possano rappresentare un insieme di campioni della massa inerziale di riferimento.

Il secondo passo consisterà nel verificare che lo strumento di misura rispetti la proprietà additiva  della massa inerziale, come prevista dal modello dell’oscillatore armonico, ossia che il  \(T^2\) dipenda linearmente dal numero n di masse campione (cioè oggetti tutti uguali) posti sulla bilancia inerziale:

\[T^2 = m \cdot n + b\ \ \  [1]\]

  I valori ottenuti sono riportati sul grafico seguente: notare che la retta interpolante ha un valore dell’intercetta diversa da zero; questo perché la massa inerziale del vassoio portapesi non è trascurabile rispetto alla massa inerziale dei pesi campione utilizzati.

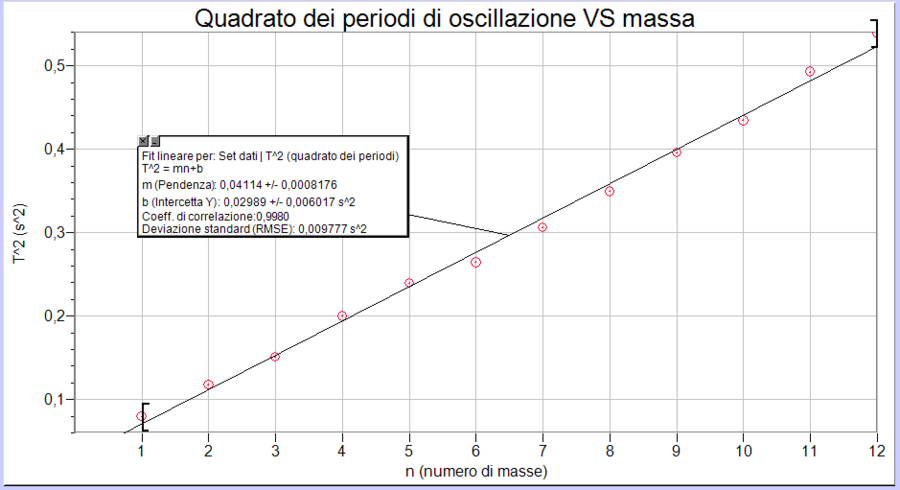
Eseguendo una regressione lineare si ricavano i valori dei coefficienti m e b della relazione [1], che nel caso in esame risultano essere: \(m = (0.0411 \pm 0.0008) \frac{s^2}{m.c.}\) e \(b= (0.030 \pm 0.006) s^2\) dove m.c. indica l’unità di misura della massa inerziale, assunta nel nostro caso pari alla massa inerziale dei pesetti tutti uguali utilizzati.

Misura della massa inerziale
Si è ora pronti a misurare la massa inerziale di un corpo qualunque in termini della massa inerziale del peso campione. 

Per misurare la massa inerziale di un corpo, basterà inserirlo sul vassoio e calcolare il periodo di oscillazione.

Ad esempio se T= (0.51 ± 0.01)s  invertendo la relazione [1] si ottiene 

\[n=  \frac{T^2}{m} – \frac{b}{m}   = 5.6\ m.c.\]

con incertezza 

\[\Delta n = \sqrt{\left( 2 \frac{T}{m} \Delta T \right)^2 + \left( \frac{T^2}{m^2} \Delta m \right)^2 + \left( \frac{\Delta b}{m}\right)^2 + \left( \frac{b}{m^2} \Delta m \right)^2 } = 0.3\ m.c.\]

\[n = (5.6 \pm 0.3)\ m.c.\]

Confronto tra massa inerziale e massa gravitazionale
L’attività può essere conclusa chiedendo di confrontare la massa inerziale di due corpi con quella gravitazionale: le due masse sono distinte nei loro effetti, e quindi nel metodo di misura.

Dopo aver misurato con la bilancia inerziale le masse di due corpi A e B (\(m_A\) , \(m_B\)) in unità m.c. si procede a misurare la massa gravitazionale dei due corpi A e B con una bilancia comune ottenendo i risultati \(\overline{m}_A\) e \(\overline{m}_B\).  

I risultati sperimentali conducono a stabilire che il rapporto tra le masse inerziali dei due corpi A e B è uguale al rapporto tra le loro masse gravitazionali. In altre parole, è  

\[\frac{m_A}{\overline{m}_A} = \frac{m_B}{\overline{m}_B} = cost\]

ossia il rapporto tra massa inerziale e gravitazionale ha, per qualunque corpo entro gli errori sperimentali, lo stesso valore. 

A questo punto si fa osservare che, se supponiamo che il corpo B sia il campione depositato a Sèvres e che esso sia stato scelto come campione di massa unitaria anche per le masse inerziali, valgono le relazioni:

\[\frac{m_B}{\overline{m}_B} = 1 \quad ; \quad  \frac{m_A}{\overline{m}_A} = 1\]

E’ quindi sufficiente scegliere per massa inerziale e massa gravitazionale la stessa unità di misura, il chilogrammo, e le misure della massa inerziale e della massa gravitazionale di uno stesso corpo saranno espresse dallo stesso numero.

Note e storia

Storia

L’uguaglianza tra le due masse fu verificata già da Newton mediante esperienze sui pendoli. Tali esperienze avrebbero permesso di mettere in evidenza una eventuale differenza tra le due masse dell’ordine di 1 su \(10^3\). Esperienze molto più recenti e più raffinate, eseguite da Eötvös nel 1922 hanno potuto stabilire l’identità delle due masse dell’ordine di 1 parte su \(10^9\). Ulteriori esperienze, condotte da R. Dicke, hanno permesso di accertare che la massa inerziale può differire da quella gravitazionale solo per meno di 3 parti su \(10^{11}\) e alcune, recentissime, di 1 parte su \(10^{13}\).

Questa identità, che per la fisica classica può rappresentare un fatto puramente accidentale, si è invece rivelata, attraverso le considerazioni critiche di Einstein, fornita di un profondo significato, nel quadro della teoria generale della relatività. In tale ambito, l’affermazione dell’identità tra massa inerziale e massa gravitazionale costituisce il cosiddetto principio di equivalenza.

Nota
L’esperimento fa parte di una collezione di esperienze di laboratorio elaborate nell’ambito del  progetto  “Nuove idee per la didattica laboratoriale nei Licei Scientifici” finanziato dal MIUR.

Bibliografia

• R. v. Eötvös, D. Pekár, E. Fekete, Annalen der Physik (Leipzig) 68, 11, 1922; 
• P. G. Roll, R. Krotkov, R. H. Dicke, Annals of Physics, 26, 442, 1964. 

Autori

Diener Paola
Ciardiello Eduardo

Specifiche esperimento Materia Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Due piattelli, due lame di sega per metalli, bulloni, bilancia Durata esperimento in classe 2 h Capacità di bricolage/assemblaggio Sì Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone Sì Parole chiave Meccanica Dinamica del punto materiale Massa inerziale Oscillatore armonico