Riassunto / Abstract

Le attività di simulazione si rendono necessarie per l’Astronomia, una materia formativa ma difficile da trattare nelle ore mattutine in modo sperimentale.

L’attività è rivolta agli studenti del primo anno ed è finalizzata alla comprensione e utilizzazione del metodo scientifico. 

Gli allievi saranno stimolati a comprendere l’importanza dell’osservazione del cielo, come hanno fatto innumerevoli generazioni dall’antichità alla prima metà del XX secolo, per trarre delle informazioni sull’importanza della scoperta. Inoltre saranno guidati all’utilizzazione dei punti di riferimento astronomici, per l’orientamento e il computo del tempo. Si procederà quindi all’osservazione dei sistemi di riferimento astronomici con i programmi Stellarium o Celestia o Skymap pro (quest’ultimo preferito dall’Autore) e dei simulatori e demo inclusi.

Scheda sintetica delle attività

Vengono discussi i modi per trovare i punti di riferimento astronomici e viene dimostrato il loro significato astronomico e geografico e le finalità pratiche utilizzando i simulatori virtuali. Questo permette di familiarizzare con conoscenze che gli uomini hanno acquisito attraverso i secoli, commettendo errori ma spinti dalla curiosità e dalla soddisfazione della dimostrazione. È sempre stato un ottimo approccio al metodo scientifico da proporre proprio nelle classi prime, senza scendere nei particolari dell’Astronomia sferica.

• L’ombra minima staccata da uno gnomone (per tracciare la linea meridiana e la misura del tempo).
• La ricerca della Stella Polare (per l’orientamento geografico e astronomico).
• L’osservazione del moto dei corpi celesti nel sistema solare.
• Cambiare pianeta!

Risorse necessarie

• Computer e/o LIM;
• sofware Stellarium o Celestia o Skymap pro8;
• http://www.solarsystemscope.com/ (in italiano);
• http://astro.unl.edu/animationsLinks.html (in inglese);

(tempi necessari da 4 a 7 ore, ma alcune simulazioni possono essere fatte anche a casa)

Prerequisiti necessari

• Capacità di calcolo matematico;
• conoscenza della differenza tra misure lineari e angolari;
• capacità di usare un programma di simulazione al computer sia in rete che offline.

Obiettivi di apprendimento

• Capacità di osservazione e misurare;
• capacità di dimostrare leggi empiriche e teoriche;
• riflessione e curiosità  per l’indagine scientifica.

Dotazioni di sicurezza

Nessuna

Svolgimento

Brainstorming

D. Che cos’è un punto di riferimento?

R. Un luogo fisso

D. Per esempio?

R. La scuola è il nostro punto di riferimento, ma anche la professoressa!

D. Più la scuola o la professoressa?

R. E’ uguale

D. No, non proprio, cosa succederebbe se la professoressa fosse mandata in pensione o andasse in un’altra scuola, voi andreste con lei o rimarreste a scuola?

R. Rimaniamo a scuola, ho capito, allora il punto di riferimento deve stare fermo!!!

D. Certo! In cielo o in Terra ci sono punti di riferimento facendo finta di non avere a disposizione né case, né orologi, né calendari, nulla,  solo noi nel territorio magari sconosciuto.

R. Se siamo in un bosco o su un’isola deserta non ci sono punti di riferimento, solo il sole, ma si muove.

D. Meglio cercarli di giorno o di notte?

R. Sicuramente di giorno o no?

R. Di notte si vedono tante stelle ma io so che una sta ferma, però  non so mai trovarla.

D. La Terra è divisa in due emisferi e nel nostro il Boreale si vede, cercandola, una stella molto particolare.

R. La stella polare! Sta sopra il Polo Nord!

D. Perché è particolare?

R. Perché sta ferma? Ma perché sta ferma, se le altre ruotano come fa il sole?

D. Dipende dai punti e dai sistemi di riferimento, per noi appare ferma perché si trova sul prolungamento dell’asse terrestre e noi le giriamo sotto.

R. Come si fa a vedere questo?

D. Cominciamo isolando le variabili da cercare e da misurare cioè il luogo, e il tempo inteso come  l’ora e il giorno

Attività 1 (simulatore 1-2 ore)

L’ombra minima                                                                                                                                   

D. I più semplici punti di riferimento per un uomo che fa un’osservazione del cielo quali sono?

R. Non saprei, forse il terreno stesso su cui poggiamo i piedi!

D. Certo il piano dell’orizzonte è il primo punto di riferimento solidale con i piedi e poi?

R: La testa forse?

D. proprio così, la testa indica un punto detto Zenith, questo compone il nostro sistema x,y,z che ci segue per qualunque osservazione o misura, cominciamo con il simulatore.

http://astro.unl.edu/classaction/animations/coordsmotion/transitmovie.html

http://astro.unl.edu/classaction/animations/coordsmotion/sunpaths.html

http://astro.unl.edu/classaction/animations/coordsmotion/sunmotions.html

Grazie al simulatore i ragazzi possono provare a variare il luogo, il tempo (ora del giorno o giorno dell’anno) dell’osservazione e studiare il significato dell’ombra minima per un emisfero e per l’altro per arrivare alla deduzione che l’ombra minima di uno gnomone indica sempre il NORD nell’emisfero boreale e il SUD in quello australe.

Viene così identificata, nel piano sotto lo gnomone (o sotto un ipotetico osservatore), la retta che congiunge i due punti: ombra minima-gnomone che prolungata individua il sud e la perpendicolare, giacente sullo stesso piano, che identifica l’EST e l’OVEST. Abbiamo così dimostrato come si trovano i punti cardinali.

Attività 2 (simulatore 1-2 ore)

La ricerca della Stella polare
http://astro.unl.edu/classaction/animations/ancientastro/dipperclock.html
http://astro.unl.edu/classaction/animations/coordsmotion/radecdemo.html

Uso di Skymap

Identificata la stella polare grazie alle stelle Dubhe e Merak Ursae Maioris (i due puntatori) si procede così: mettere in rotazione oraria ed identificare il punto che sta fermo.

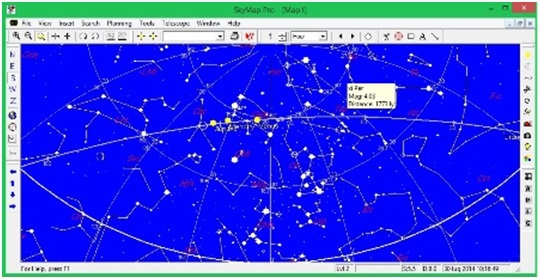
Quando si apre SkyMap, esegue l’ora del giorno e la data in cui siamo, e visualizza sullo schermo la mappa celeste, per “default” alla latitudine di Londra. La mappa mostra la vista del cielo verso sud per qualsiasi ora e data. Alcune stelle sulla carta sono collegate da linee. Queste linee formano ” Figure” che rappresentano delle costellazioni. A seconda dell’ora e della data – il Sole, la Luna o pianeti possono essere visibili sulla carta. La “linea spessa curva” lungo la parte inferiore della mappa è l’orizzonte: al di sopra di questa linea è il cielo visibile, mentre al di sotto dell’orizzonte, la porzione non visibile della sfera celeste.

Le linee curve, se in esecuzione da programma, parallele all’orizzonte, sono i cerchi di eguale altezza angolare, chiamati “almucantarat” (vedi astronomia araba), tutti gli oggetti su queste linee o cerchi, sono alla stessa distanza angolare sopra l’orizzonte (sistema di coordinate altazimutale), l’etichetta in alto a destra di ogni “incrocio”, nella griglia altazimutale, mostra l’altezza in gradi, definita “declinazione”. Il punto direttamente sopra – “zenith” – è il punto in cui tutti i cerchi di declinazione convergono. Nell’esempio proposto in figura la linea sottile che passa appena sopra Giove e Saturno è “l’eclittica”, il percorso apparente seguito dal Sole sullo sfondo delle stelle, nel corso di un anno.

I pianeti si trovano sempre vicino a questa linea, nella fascia anche chiamata “Zodiaco”.

Conclusioni
I moti di tutti gli oggetti celesti, stelle, pianeti, Sole e Luna, in funzione della latitudine dell’osservatore, possono essere circumpolari o compiere archi di cerchio con levata e tramonto (occidui).

Esempi

http://astro.unl.edu/classaction/animations/coordsmotion/celestialhorizon.html

http://astro.unl.edu/classaction/animations/lunarcycles/positionsdemonstrator.html

Attività 3 simulatore 1 – 2 ore

A. La ricerca del moto dei corpi celesti nel sistema solare (e delle Leggi)

http://astro.unl.edu/classaction/animations/renaissance/ptolemaic.html

http://astro.unl.edu/classaction/animations/renaissance/retrograde.html

http://astro.unl.edu/classaction/animations/lunarcycles/lunarapplet.html

B. La ricerca dei punti di vista delle fasi lunari e la declinazione lunare

http://astro.unl.edu/classaction/animations/lunarcycles/moonphases.html

http://astro.unl.edu/classaction/animations/lunarcycles/fullmoondec.html

http://astro.unl.edu/classaction/animations/lunarcycles/lunarphasequizzer.html

 C. simulazione riassuntiva

http://astro.unl.edu/classaction/animations/renaissance/kepler.html

Con questo ultimo link si può avere veramente una visione d’insieme dei corpi che compongono il sistema solare, si possono apprezzare in modo molto semplice le tre leggi di Keplero e anche la Legge di gravitazione universale di Newton.

Conclusioni

Si può capire in modo “visivo” cosa significa il periodo di rotazione e la distanza dei diversi pianeti nel nostro piccolo sistema solare (i loro periodi) più o meno lunghi sono determinati dalla seconda e terza Legge di Keplero).
Si può anche comprendere il significato delle fasi lunari o planetarie, e il significato delle eclissi.

Attività 4 (simulatore 1 ora)

Cambiare pianeta!

1. adesso che abbiamo capito quasi tutto della Terra e del nostro sistema solare, CAMBIAMO PIANETA!
2. Come facciamo?
3. Usiamo un altro simulatore che ci permetterà di esaminare nuovi punti di vista per arrivare a capire che la verità ha molte facce, tante quanti sono i punti di vista.
4. Allora sono infiniti.

Proviamo ad aprire    http://www.solarsystemscope.com/

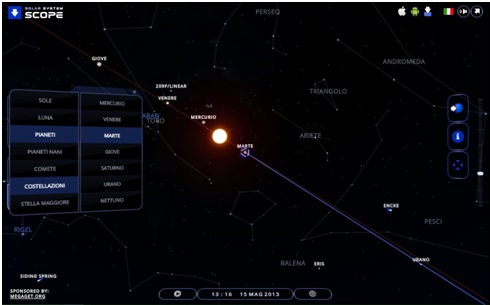
Possiamo scegliere un pianeta, un satellite, la nostra Luna o altri. Sullo sfondo si vedono le costellazioni dello zodiaco.

Conclusioni

E’ molto interessante cambiare punti di riferimento per vedere che le velocità di rotazione e le dimensioni relative cambiano di molto, questo è solo un assaggio intuitivo del significato della relatività spazio-tempo.

Note e storia

1. Il metodo suggerisce di iniziare a parlare di un certo argomento, favorendo la manifestazione delle conoscenze “ingenue” degli studenti. ( 5 minuti)
2. L’insegnante fa UNA domanda o UNA osservazione problematica.
3. Ogni studente su un foglio o sul quaderno IPOTIZZA una risposta (N:B. non deve essere solo quella che risponde alla domanda, ma deve essere una risposta dimostrabile sperimentalmente) dimostrabile con una certa azione o attività. (5  minuti)
4. I ragazzi si dispongono in gruppi già preparati e discutono con gli altri la procedura SCEGLIENDO E DEFINENDO poi una attività condivisa da tutti anche se a maggioranza. (5 minuti)
5. Si procede alla “prova” l’insegnante osserva e aiuta. ( 20 -30 minuti) non suggerisce ma può intervenire: ti ricordi cosa si voleva dimostrare? Come hai deciso di…? Come mai il risultato è diverso dall’atteso? Pensi di aver fatto tutto per bene?
6. I gruppi mostrano ed espongono (anche per scritto) agli altri, che intervengono e controllano. (10 minuti)
7. Commenti (anche a casa): quale attività ha risposto al meglio? Cosa ho imparato? Gli altri hanno fatto meglio di noi? Abbiamo scelto la via migliore tra le proposte del nostro gruppo?

Bibliografia

Bosellini Le scienze della Terra e l’universo intorno a noi Zanichelli capitolo 39,42,43,44,45,46,48;

Federici Axianas Nuovi lineamenti di geografia generale Ed Bulgarini capitolo 5,6,7;

Shipman Introduzione all’astronomia Zanichelli capitolo 2 e 3;

ESCP la Terra nello spazio C Zanichelli capitolo 19;

Dispense SAiT Firenze;

http://astro.unl.edu/animationsLinks.html;
http://www.skymap.com/smpro_main.htm;
http://www.shatters.net/celestia/;

http://www.solarsystemscope.com/;

http://www.stellarium.org/it/.

Autori

Burani Paola

Prove di verifica

• Quiz a scelta multipla

Specifiche esperimento Materia Scienze della Terra Classi a cui è rivolto 1° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano Materiale specifico Software o app Stellarium o Celestia o Skymap (gratuiti) Durata esperimento in classe 4 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Scienze della Terra Astronomia Coordinate celesti Moti della Terra e del Sole