L’attività prevede la realizzazione di un dispositivo analogico, per la visualizzazione e il calcolo della precessione equinoziale (P.E.), uno dei tre principali moti millenari del pianeta Terra, la cui scoperta, compiuta dall’astronomo greco Ipparco (II sec. A.C.) ha costituito una tappa fondamentale per lo sviluppo della scienza. Il dispositivo consente di visualizzare il fenomeno, la cui durata effettiva è di circa 25800 anni, collegando meccanicamente lo spostamento dei poli celesti, il cosiddetto “moto doppioconico”, al costante moto precessionale in senso orario dei nodi equinoziali.

Scheda esperimento
| Classi | 1° biennio |
| Tipologia | Povero |
| Durata | 1 h |
 |  |  |  |
Scheda sintetica delle attività
Si effettua in aula o laboratorio per la fase di montaggio. La disponibilità per l’utilizzazione didattica è permanente. Costituisce con un set di altri modelli e dispositivi, un ciclo di esperienze didattiche che permettono di “rovesciare” la presentazione tradizionale dei temi, costituendo la base sperimentale dell’osservazione e comprensione dei fenomeni naturali, collegati ai moti della Terra nello spazio, e all’interazione del pianeta con l’ambiente del Sistema solare, particolarmente la Luna e il Sole.
Risorse necessarie

- 1 foglio di carton plume, di dimensioni 30 x 60 cm e spessore 5 mm (nella foto sono presenti le singole componenti già ritagliate e disposte su un foglio integro al fine di visualizzare la soluzione ottimale di taglio);
- tubo (di metallo o plastica) di diametro 3 mm e lunghezza 27 cm;
- bacchetta di sezione circolare con diametro 2 mm e lunghezza di 30 cm;
- asse con diametro di 2 mm e lunghezza di 15 cm;
- colla vinilica e colla ultrarapida;
- chiodini;
- 1 rondella diametro 1.5 cm con foro di diametro di 2 mm;
- sferetta di polistirolo, diametro di 5 cm;
- fotocopie mascherine cerchi celesti e supporti (vedi allegati);
- taglierino;
- goniometro;
- pennello;
- carta vetrata;
- macchinetta fotografica.
Prerequisiti necessari
Nessuna competenza necessaria
Obiettivi di apprendimento
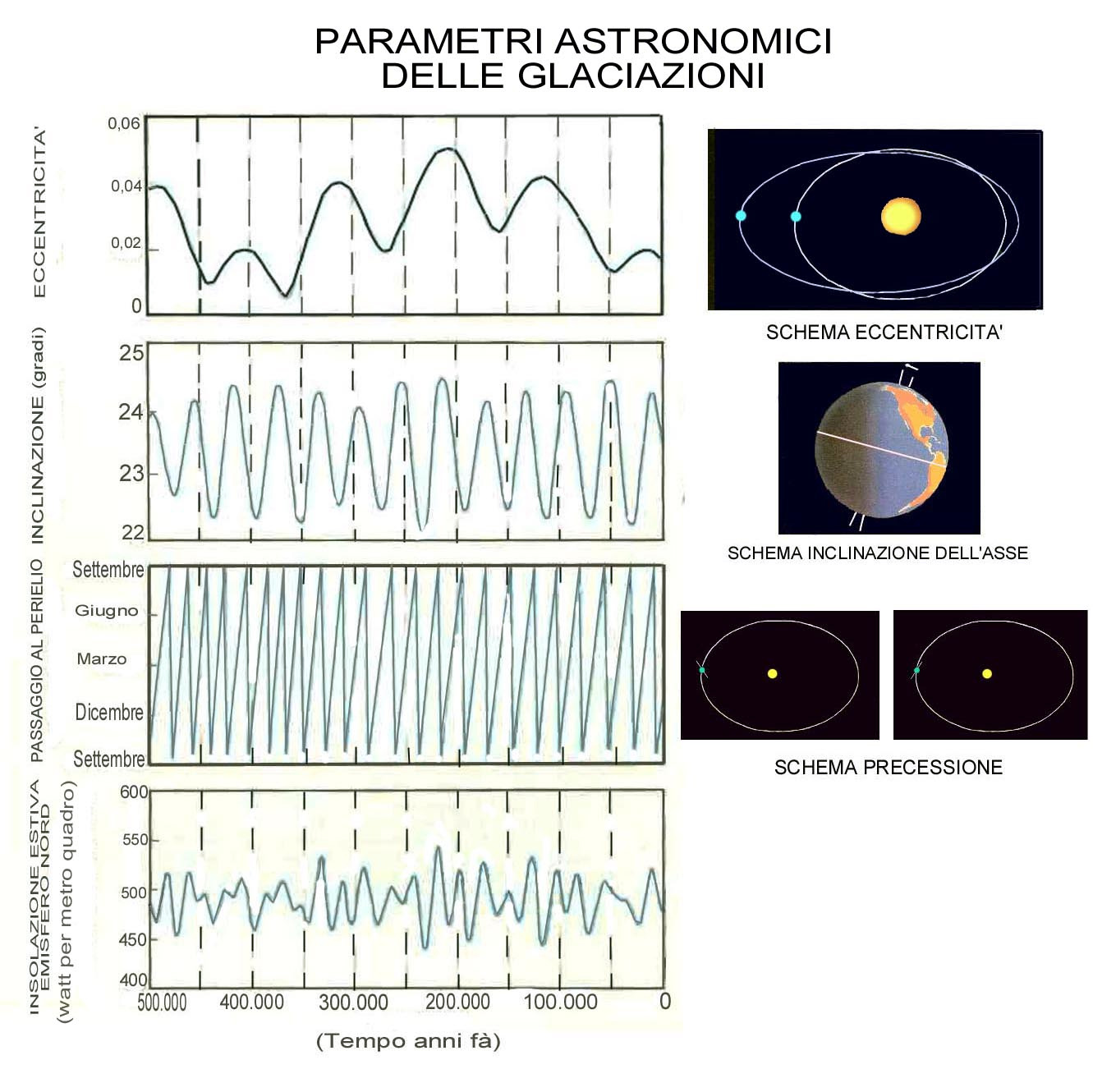
La realizzazione del dispositivo consente di “modellizzare” un fenomeno, la cui descrizione teorica prevede un elevato livello di astrazione. Gli studenti sono in grado di comprendere il significato dei principali elementi e cerchi geografici-astronomici, apprezzare visivamente il vincolo meccanico fra spostamento dei poli e precessione equinoziale, di comprendere il fondamentale ruolo dell’obliquità del pianeta per il verificarsi del fenomeno precessionale, di accedere al concetto di “tempo profondo”, alla base delle scienze geologiche e astronomiche. Insieme il modellino evidenzia l’alternanza delle posizioni dei solstizi e degli equinozi, che modulano l’irradiazione solare degli emisferi, componente fondamentale della teoria astronomica delle glaciazioni di M. Milankovitch (figura 2).
Dotazioni di sicurezza
Nessuna
Svolgimento
Realizzazione del dispositivo
- Si dispongono i componenti e i materiali da utilizzare (figura 1).
- Si effettuano i tagli dei due elementi del supporto (allegati 1 e 2), incollando le relative mascherine, si assemblano collocandoli nelle rispettive asole (figure 3-6).




- Si ritagliano le mascherine del cerchio eclitticale (allegato 3) avente diametro massimo 25 cm circa/diametro minino 20 cm circa (figura 7) e del cerchio equatoriale (allegato 4) avente diametro massimo 19 cm/diametro minimo 5 cm (figura 8).
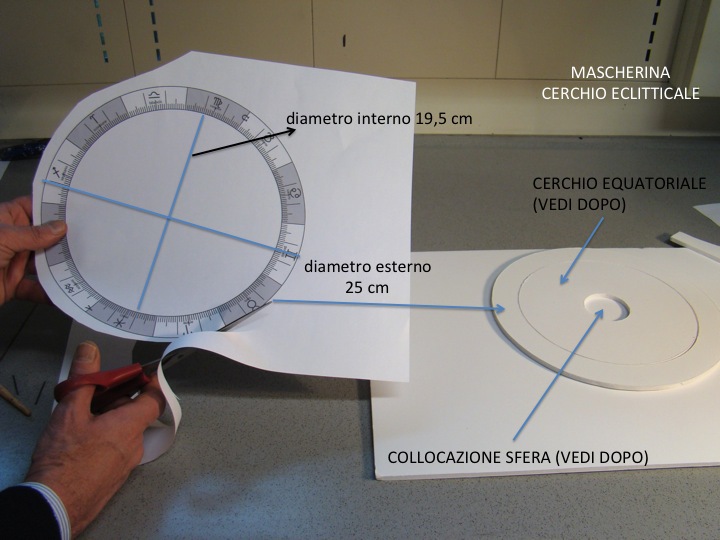

- Si incollano le relative mascherine ai cerchi equatoriale e eclitticale sul carton plume e si ricavano le relative componenti (esempio in figura 9).

- Si ritaglia la mascherina del cerchio precessionale (allegato 5) di diametro 10 cm (figura 10) e si incolla sul carton plume ritagliando la componente (figura 11).


- In figura 12 è riportato il risultato finale della preparazione dei singoli componenti.
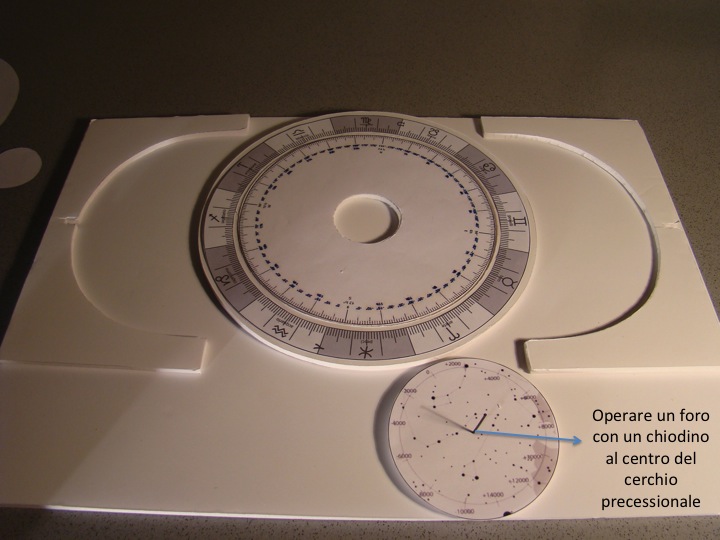
- Si fissa il cerchio eclitticale al supporto del modello (figura 13) facendo in modo che il punto di Gamma (o punto dell’Ariete) e il punto della Bilancia siano incollati sui supporti (figura 14).


- Si posiziona l’asse di lunghezza 30 cm (asse eclitticale), al centro del supporto (figure 15-18).




- Si colloca la rondellina come nella foto (figure 19 e 20); la rondellina è necessaria per non far cadere il tubicino di metallo.


- Si effettua l’inserimento del tubicino di metallo (che verrà successivamente inserito sull’asse eclitticale), nella sferetta avendo cura che sia passante per il centro, individuando così i due poli geometrici (figure 21 e 22). Per identificare i due poli opposti della sfera si può ricorrere all’ausilio di un regolo (calibro). Produrre il foro progressivamente con l’aiuto di un chiodo.


- Si colloca la sferetta rappresentante la Terra, nel foro del cerchio equatoriale.
- Si effettua il posizionamento del semiasse polare, passante per il piano N-S (da visualizzare sul cerchio equatoriale) (figura 23) imponendo un angolo di 23° rispetto all’asse eclitticale (anche questo contenuto nel piano NS sul cerchio equatoriale). SI avrà cura inoltre, con l’utilizzo del goniometro, di disporre il cerchio equatoriale perpendicolare all’asse polare (come illustrato in figure 23 e 24).
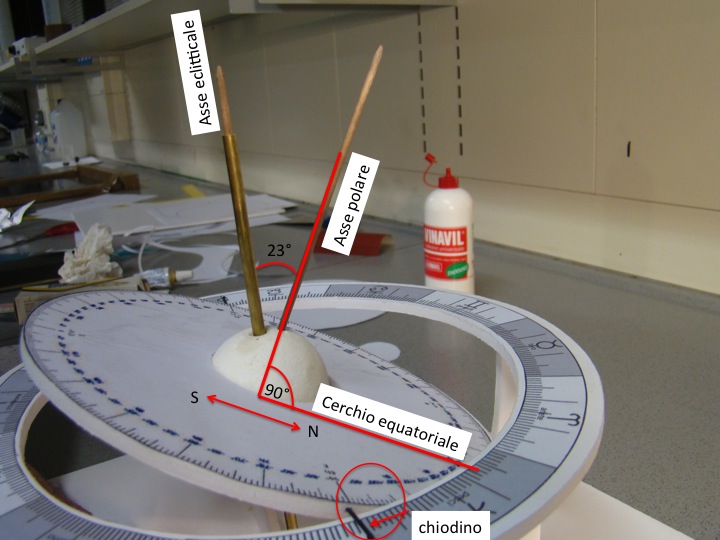
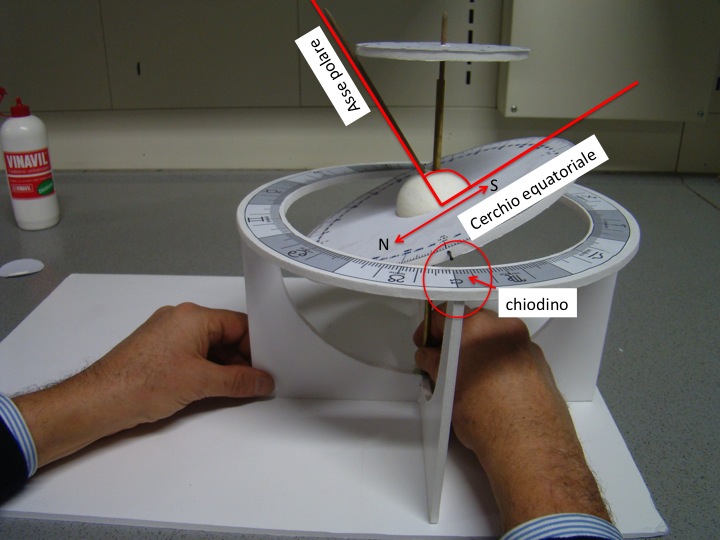
- Si inseriscono i chiodini con funzione di “lancetta”, nelle posizioni corrispondenti ai punti Gamma (EST) e Bilancia (OVEST) del cerchio equatoriale (figure 23-25). Fondamentale che l’asse cavo (tenuto in foto 23 con la mano destra dell’operatore) sia libero di ruotare. Inoltre, i chiodini devono essere allineati e permettere al cerchio equatoriale di muoversi liberamente all’interno del piano equatoriale.

- Si sistema il cerchio precessionale alla sommità dell’asse fisso (asse eclitticale, figure 24-25) avendo cura che il semi-asse polare sia tangente al cerchio stesso in corrispondenza dell’attuale Stella Polare (+2000).
- Le posizioni dei due cerchi eclitticale e equatoriale e del cerchio precessionale devono coincidere come evidenziato nelle foto, posizione corrispondente all’assetto celeste attuale (figura 25).
Esempi di come si utilizza il modello della precessione
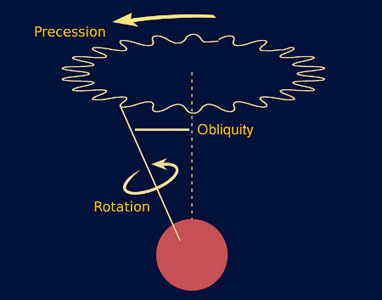
Il modellino presenta il fenomeno della precessione evidenziando, tra le caratteristiche che la rendono possibile, l’inclinazione dell’asse terrestre (OBLIQUITA’), il vincolo geometrico-meccanico fra il moto doppio conico, e la precessione oraria dei nodi equinoziali. A titolo di esempio sono illustrate alcune applicazioni di carattere astronomico e storico.
Esempio A (figura 26): Partendo dalla posizione attuale: per l’emisfero boreale, il polo celeste nord indicato dalla stella Polare, i nodi equinoziali nei Pesci e nella Bilancia (figura 25), giriamo in senso antiorario l’asse cavo mobile di circa 60°. Il moto antiorario porta all’indietro l’asse di rotazione del pianeta che costituisce la lancetta dell’orologio astronomico nel cerchio precessionale superiore, e ci posizionamo nel punto intermedio fra le posizioni -2000 A.C, -4000 A.C. Si nota che la stella polare all’epoca era α Draconis, la Thuban degli arabi; contemporaneamente è mutata la posizione dei nodi “γ” e “Ω”, che si trovano rispettivamente nella costellazione del Toro e Scorpione.
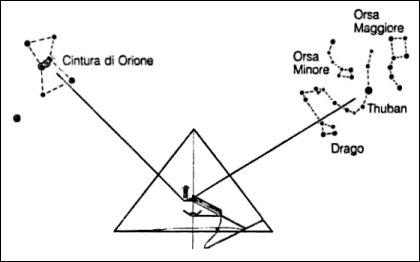
Si possono effettuare delle considerazioni di carattere storico e archeologico: la stella Thuban era l’astro verso cui era rivolto lo speciale canale presente in molte piramidi (figura 27 e 28), collegante la camera sepolcrale alla superficie del monumento. Il canale aveva significati magico-religiosi inerenti la sopravvivenza ultraterrena.
La posizione dell’equinozio di primavera in Toro si è riflessa in monumenti e raffigurazioni artistiche diffuse in tutto il vicino oriente e Mediterraneo orientale. A titolo di esempio si citano i bassorilievi con tori nelle porte di Persepolis, Ninive. La memoria del lungo periodo in cui le civiltà agricole della mezzaluna fertile hanno legato i riti della primavera al culto del toro ha avuto importanti riferimenti nelle letterature e nei miti religiosi e ha lasciato una traccia profonda, come si osserva nel successivo esempio.


Esempio B (figura 29): Si ruota l’asse cavo in senso orario di circa 30°, la lancetta dell’asse terrestre si posiziona circa all’anno 0. Il polo celeste nord si è avvicinato alla costellazione dell’Orsa minore, ma la stella polare attuale ne è ancora lontana di circa 5°. Nel II sec A.C. venne scoperto e descritto dall’astronomo Ipparco, il fenomeno della precessione (vedi note storiche). La costellazione dell’equinozio di primavera era l’Ariete. Il fenomeno del passaggio del nodo equinoziale dal Toro all’Ariete, stupì astrologi e sacerdoti, che cercarono una spiegazione religiosa al fenomeno. La spiegazione venne identificata nello schema di costellazioni osservabili, prossime a quella del Toro, tra queste la costellazione chiamata Perseo, che era associata all’antica divinità iranica, Mithra. Nacque così, in Anatolia, probabilmente a Tarso in Cilicia, la religione Mitraica, basata sull’osservazione di un fenomeno astronomico, e ricca di riferimenti e simbolismi celesti. Il dio Mitra-Perseo sacrificava il Toro celeste, e il sangue di quest’ultimo rinnovava la fertilità della terra. Il dio era molto potente, perché in grado di muovere i cardini e l’asse della sfera celeste, cioè dell’universo conosciuto. Il mito cosmogonico era dunque una “tauroctonia” (figura 30), sacrificio rituale che affonda in radici lontane e che si è protratto, in vari modi, fino ai nostri tempi: p.e. le corride (purtroppo!). Altri simbolismi astronomici che rimandano agli equinozi, sono presenti nelle raffigurazioni pervenute delle tauroctonie: p.e. nelle rappresentazioni di Cautes e Cautopates, i “dadofori”, le cui gambe si incrociano a simboleggiare proprio i nodi equinoziali.(La religione mitraica, che era un culto di “salvezza”, si diffuse rapidamente in tutto l’impero, con alcune notevoli eccezioni, p.e. l’Egitto e l’Africa settentrionale. Ha lasciato ampie testimonianze archeologiche, infatti i mitrei sono diffusi da Carrawburgh (Brocolitia) (figura 31), al confine fra l’Inghilterra e la Scozia, fino a Dura Europos al confine fra la Siria e l’Iraq, nella sola Roma se ne contavano alcune centinaia).



.
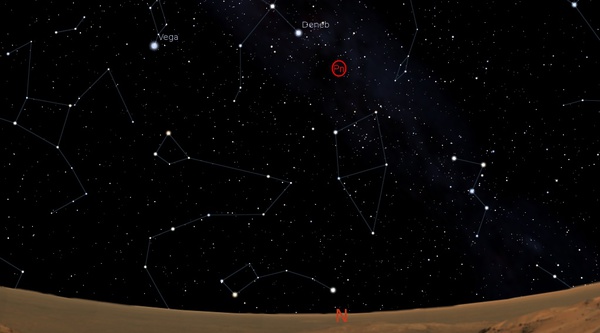
Esempio C (figura 32): Si ruota l’asse cavo in senso orario di circa 180°, e la lancetta dell’asse di rotazione si posiziona fra le date 12000 D.C. e 14000 D.C.. In quel lontano futuro, la Terra avrà il suo polo celeste nord molto prossimo alla stella α Lyrae, la gigante azzurra Vega. La posizione delle stagioni lungo l’orbita sarà invertita rispetto all’attuale: avremo il pianeta all’afelio in prossimità del solstizio invernale, e al perielio in coincidenza del solstizio estivo. Nella Teoria astronomica delle glaciazioni di M. Milankovitch, tale posizione favorisce, in concomitanza di altri fattori, l’optimum climatico per le latitudini medio-elevate dell’emisfero settentrionale, emisfero leader per il corso dei mutamenti ciclici climatici. Con riferimento al pianeta Marte l’attuale asse di rotazione, nell’emisfero settentrionale, è rivolto a una posizione prossima ad α Cygni, la supergigante azzurra Deneb, che è dunque la stella polare delle notti marziane (figure 33-35), e lo diventerà per la Terra fra circa 9 mila anni: l’asse polare di Marte ha quindi un orientamento spaziale, quasi opposto a quello del nostro pianeta. Gli effetti climatici e geologici del moto precessionale su Marte, sono assai più rilevanti che sul nostro pianeta.


Note e storia
NOTE PER LA REALIZZAZIONE
Lo scopo di questo modellino è la visualizzazione del fenomeno della P.E., nelle sue due componenti fondamentali: lo spostamento millennario dell’intersezione dell’asse di rotazione della Terra con la sfera celeste, il cosiddetto moto doppioconico dei poli, e la precessione dei nodi equinoziali. Il modellino ha come piano fondamentale quello dell’eclittica ovvero il piano dell’orbita terrestre, il suo asse è costituito dall’asse cavo e dall’asse interno. La funzione dell’asse cavo, libero di girare con la sferetta terrestre, è di rappresentare il reale moto millennario del pianeta. L’asse interno fisso che reca il disco precessionale e le date delle epoche, rappresenta l’asse del piano dell’orbita della Terra. L’equatore celeste rappresentato dal corrispettivo cerchio, è suddiviso nelle tradizionali costellazioni zodiacali, ed è libero di ruotare completamente. Su di esso, nella realtà sul rigonfiamento equatoriale del pianeta si esercita l’attrazione gravitazionale lunisolare, responsabile del moto precessionale e doppioconico. Il modellino evidenzia l’impossibilità del fenomeno precessionale su un pianeta con l’asse di rotazione normale al piano orbitale: l’equatore celeste e l’eclittica sono coincidenti, non esistono pertanto i nodi. Nella realtà è necessario anche che il pianeta presenti uno schiacciamento equatoriale, conseguenza del rapido moto di rotazione sul proprio asse, e delle caratteristiche di un interno planetario differenziato.
NOTE STORICHE
La scoperta della P.E. ha costituito uno dei massimi risultati dell’Astronomia e della Geografia scientifica ellenistiche. Ipparco, astronomo, geografo e fisico (Nicea-Rodi, circa 190-120 A.C.), giunse all’identificazione del fenomeno, conseguentemente alla realizzazione di un catalogo astronomico di circa mille stelle, con elevata precisione (1/6 di grado), osservabili alla latitudine di Rodi. Non essendo pervenute le opere di Ipparco, con l’eccezione del “Commento ai fenomeni di Arato”, i dettagli tecnici di questa imponente opera, si rinvengono nell’Almagesto di Tolomeo (II sec. D.C.) (Figura 8). Ipparco confrontando i dati del suo catalogo, con le posizioni di stelle in precedenti cataloghi (p.e. a Virginis, Spica), quelli degli astronomi alessandrini Timocari (Alessandria, circa 320-260 A.C.) e Aristillo (Samo, circa 320-260 A.C.), rilevò che mentre i valori delle declinazioni celesti erano coincidenti, quelli delle longitudini eclitticali erano tutti affetti da una stessa variazione, pari a circa 2°. Ne dedusse che la causa del fenomeno, doveva trovarsi nello spostamento dell’origine del sistema di coordinate astronomiche, ovvero il cosiddetto “punto di gamma” o “primo d’ariete”, per cui passa il meridiano fondamentale celeste. La scoperta è da collocarsi verosimilmente nel periodo 140-130 A.C.. L’identificazione della precessione equinoziale non influenzò esclusivamente i circoli scientifici del mondo ellenistico. Pochi decenni dopo iniziò a diffondersi dalla Cilicia (odierna Turchia), nel mondo mediterraneo, il culto del dio Mitra, una religione basata su una complessa simbologia astrologica-astronomica-cosmogonica. I mitrei, luoghi di culto della religione, attestano la ricchezza dei riferimenti astronomici, in particolare il cuore dei misteri mitraici è costituito dalla cosiddetta “tauroctonia”. Il simbolismo mostra il Dio Mitra nell’atto di sacrificare un toro. Tutti gli elementi della scena hanno precisi riferimenti a una mappa celeste, così come si presentava il cielo all’equinozio di primavera nel 2200 A.C.. L’intera religione, divenuta culto principale in epoca imperiale, era fondata sul passaggio dell’equinozio di primavera dalla costellazione del Toro all’Ariete che si era verificato circa due millenni prima. Altri riferimenti della scoperta della precessione si rinvengono in realizzazioni architettoniche e artistiche.

Bibliografia
- Romano Giuliano, “Introduzione all’Astronomia”, Franco Muzzio Editore
- Schroeter Walter, “Astronomia Pratica”, Longanesi Editore
- Ulansay David, “La religione mitraica”, Edizioni Mediterranee
- AA.VV., “Shadows”, programma freeware
- Video che permette di visualizzare la precessione equinoziale
Autori
Chirri Maurizio
Parotto Maurizio
Schede / Allegati
- Allegato 1 – prima struttura di sostegno
- Allegato 2 – seconda struttura di sostegno
- Allegato 3 – cerchio eclitticale
- Allegato 4 – maschera del cerchio equatoriale
- Allegato 5 – cerchio precessionale