Riassunto / Abstract
E’ lecito interpolare tra le divisioni della scala di uno strumento analogico?
In questo articolo impariamo cos’è l’errore di lettura, a valutarlo sperimentalmente e come usarlo. Vediamo cosa dicono le direttive del BIPM (Bureau International des Poids et Mesures) e forse scopriamo qualche cosa di nuovo.
Scheda sintetica delle attività
- Si propone di ragionare sperimentalmente sul significato di errore di lettura utilizzando il senso comune e confrontandosi con i libri di testo e le direttive internazionali.
- Si propone di leggere tra le divisioni di una scala come metodo per stimare l’errore di lettura da uno strumento analogico
- Si discutono i risultati, si confrontano con le indicazioni del Bureau International des Poids et Mesures e se ne traggono le conclusioni.
- Si stabilisce che l’errore di lettura deve indicare con quale accuratezza siamo in grado di leggere la scala dello strumento. Anche se l’errore di lettura è usualmente considerato come metà della minima divisione della scala, gli esperimenti proposti mostrano che esso può essere effettivamente molto minore di così. Si riconosce quindi una forte componente soggettiva nel definire l’errore di lettura in funzione di quanto accuratamente l’operatore ritiene di essere in grado di leggere tra le tacche.
Risorse necessarie
- Stampa delle figure allegate o carta e penna per realizzarne di simili.
- è utile l’uso di fogli elettronici (Office, OpenOffice, LibreOffice) per un più rapido trattamento dei dati
- strumenti di misura analogici;
- può essere utile il calibro millesimale descritto in 3-Fisica.
Prerequisiti necessari
- Saper calcolare valori medi di N misure;
- sapere cos’é la varianza e la deviazione standard;
- è utile saper utilizzare un foglio elettronico.
Obiettivi di apprendimento
- Saper leggere in modo critico definizioni e affermazioni riguardanti l’errore di lettura utilizzando un metodo sperimentale per la valutazione degli errori di lettura e per la verifica di ipotesi;
- riconoscere e trattare l’errore di lettura secondo le direttive internazionali (BIPM);
- comprendere l’importanza di aspetti soggettivi (quali: capacità, esperienza, abilità, fiducia, etc…) come parte fondamentale nel processo di misura e interpretazione dei dati sperimentali.
Dotazioni di sicurezza
Nessuna
Svolgimento
Nota: nel testo indicheremo con D.numero possibili spunti di discussione in aula o domande da porre alla classe.
Introduzione
Nel riportare la misura di una grandezza fisica è obbligatorio riportare l’errore di misura, esso ci fornisce indicazioni riguardo alla qualità della misura. Senza queste informazioni i risultati di una misura non possono essere né confrontati tra loro né confrontati con riferimenti o standard [GUM]. Sono diversi i fattori che influenzano accuratezza e precisione di una misura, qui ci occupiamo di errori di lettura e, in particolare, di errori di lettura nel caso di strumenti analogici (calibri, metri, orologi, scale graduate etc…).
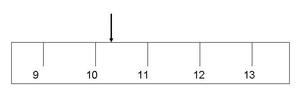
Per inquadrare il problema consideriamo la figura 1: l’indice di uno strumento analogico si trova tra 10 e 11,
D.1: quale valore associare alla misura? Quale incertezza? (può essere utile per la discussione raccogliere in una tabella le risposte della classe). Confrontando le letture degli studenti si riconosce una certa variabilità dei risultati. A ciascuno si chiede un errore da associare alla lettura, oppure un intervallo di valori entro il quale si ritiene sia il valore giusto.
In molti testi si trovano forme alternative di un’affermazione del tipo:
in uno strumento analogico le divisioni della scala (volgarmente tacche) definiscono un intervallo minimo al di sotto del quale non ha senso affinare la lettura. Indicando con
Avendo a che fare con scale molto fitte sembra un’affermazione abbastanza ragionevole, tuttavia non può essere presa come criterio assoluto. Ritengo che in pochi abbiano risposto alla D.1 con \(x = 10.0 \pm 0.5\) oppure \(x = 10.5 \pm 0.5\) infatti è abbastanza evidente che la posizione del cursore è maggiore di 10.2 e minore di 10.4.
D.2: che ne dice la classe? In che intervallo ciascuno ritiene si trovi il valore giusto?
Misura 1
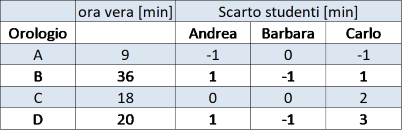
Facciamo un esempio: consideriamo un orologio che riporti solo le tacche in corrispondenza delle 3, 6, 9 e 12 (figura 2) quanti minuti indica la lancetta in A, B, C e D?
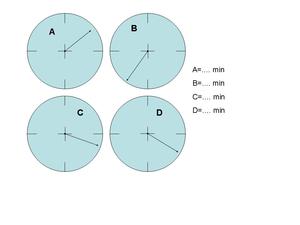
Probabilmente siamo in grado di stabilire l’ora con uno scarto ben inferiore a 5 minuti (quindi meno di
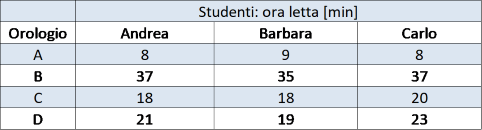
Tabella 1: lettura dell’orologio di figura 2 da parte di tre studenti
Se confrontiamo i valori letti con i valori “veri” (che possiamo valutare sovrapponendo un goniometro agli orologi come mostrato in figura 3) scopriremo che molte letture hanno uno scarto (differenza tra valore letto e valore vero) inferiore ai due minuti (quindi
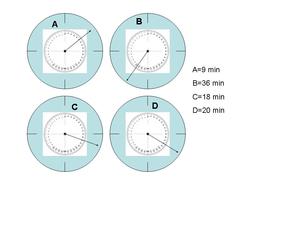
E’ chiaro quindi che assegnare un errore alla lettura degli orologi di
D.3: Quale è l’errore da associare ad una lettura di un orologio come quelli di figura 2?
Ovvero, dal momento che abbiamo detto nell’introduzione che l’errore di misura deve fornire indicazioni riguardo alla qualità della misura, se chiedo ad Andrea, Barbara o Carlo (in una classe avremo molta più celta) di leggere l’ora dall’orologio mostrato in figura 4, da chi mi aspetto una lettura di migliore qualità? Chiaramente non mi fido di tutti e tre allo stesso modo: guardando agli scarti ottenuti dai tre Barbara sbaglia mediamente meno degli altri e Carlo più degli altri.
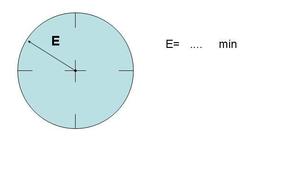
Tabella 3 mostra la lettura dell’ora dell’orologio E fatta dai dei tre studenti.

D.4: La discussione dovrebbe portare a riconoscere che l’errore di lettura dipende da chi legge! (nota 2).
D’altronde non è difficile convincersi che nel considerare una lettura è più facile dare fiducia ad un tecnico esperto che conosce bene lo strumento piuttosto che di un giovane alle prime esperienze. Quindi in base alla lettura degli orologi A,B,C,D mi fido di più di Barbara. Per quantificare questa fiducia devo fornire un numero, la domanda è:
D.5: quanto vale l’errore da associare alle letture dell’orologio di figura 4 effettuata da Andrea, Carlo o Barbara? Di sicuro serve un criterio condiviso per confrontare la lettura di Barbara con quella di un altro studente che ripetesse un esperimento analogo in futuro. Su questo punto è utile una discussione per chiarire i punti di vista e cercare una strada verso la soluzione. Ad esempio utilizzare lo scarto massimo come stima dell’accuratezza delle letture di uno studente è poco ragionevole: gli estremi sono valori probabilmente dovuti a distrazione, sicuramente rappresentano una sovrastima dell’errore. Nella valutazione della bravura di uno studente a leggere tra le divisioni, bisognerebbe trovare il modo di utilizzare tutti i dati non solo i valori estremi.
Tutto questo sembra aumentare la confusione piuttosto che diradarla: se l’errore di lettura deve fornisce indicazioni chiare riguardo alla qualità della misura, come si concilia con la soggettività appena sottolineata? DI questo discutiamo più avanti. Intanto cerchiamo di capire cosa significa mi fido di più di Barbara che non di Carlo. Ho bisogno di un numero che quantifichi questa fiducia.
Cosa dicono le direttive internazionali?
Definizione di errore nelle direttive internazionali (BIPM)
Il Bureau International des Poids et Mesures (BIMP) è l’organismo preposto ad assicurare l’uniformità delle misure in ambito internazionale: the task of the BIPM is to ensure world-wide uniformity of measurements and their traceability to the International System of Units (SI).
Il BIPM, tra le sue attività, ha stabilito le linee generali per valutare ed esprimere l’errore di misura, che sono pubblicate nella guida GUM (Evaluation of measurement data, Guide to the expression of Uncertainty in Measurement) che stabilisce criteri univoci per riportare e comparare misure e risultati sperimentali.
Per i nostri scopi possiamo fermarci all’introduzione della GUM. Qui si stabiliscono alcuni punti importanti:
- gli errori di misura si dividono in:
errori di tipo A: sono quelli che possono essere valutati utilizzando un metodo statistico
errori di tipo B: sono quelli che vengono valutati in altro modo.
A questo proposito si sottolinea la necessità di superare la distinzione tra errori casuali e sistematici, anzi è definito fuorviante e da evitare il termine: “errore sistematico”. - Per quantificare gli errori di tipo A (di solito di indicano con σ) si usa la deviazione standard della distribuzione dei risultati di una stessa misura (tralasciamo qui problemi di propagazione degli errori e misure indirette).
- Per quantificare gli di tipo B si usa una stima di quella che ci si aspetta sia la deviazione standard dei dati (di solito si indica con u). Qui le cose sono più difficili da formalizzare ma la definizione data nella GUM è abbastnza intuitiva: la stima dell’errore di tipo B deve essere fatta utilizzando tutte le informazione a disposizione del ricercatore, tra queste la propria esperienza, la confidenza con lo strumento, le proprie capacità, misure precedenti effettuate con lo stesso strumento, conoscenza del fenomeno in esame, etc… (per una discussione si vedano anche le dispense del corso del Prof. G. D’Agostino)
Vi ricordate l’affermazione: l’errore di lettura dipende da chi legge? Ebbene si: l’errore di lettura è un errore di tipo B e dipende dalla sensibilità, esperienza e confidenza con la misura e lo strumento di colui che legge! Non è un caso che l’errore di lettura su un orologio sia relativamente piccolo: molti di noi sono abituati fin da piccoli a leggere l’ora. Provate a leggere uno strumento con scala logaritmica, i risultati saranno certamente diversi! (probabilmente anche chiedendo di stabilire la posizione delle lancette degli orologi in gradi anziché in minuti darà una maggiore dispersione dei risultati).
Stima dell’errore di lettura
Utilizzando le risposte degli studenti possiamo valutare di quanto sbagliano in media. Indichiamo con Δ lo scarto (differenza) tra valore esatto
E’ ragionevole che la distribuzione degli scarti dovuti alla lettura abbia abbia media nulla. Quindi la deviazione standard della distribuzione degli scarti è:
I valori della \(\sigma\) sono riportati in tabella 4. Come prescritto dalla GUM, la \(\sigma\) rappresenta la stima dell’errore fatto dagli studenti nel leggere un orologio di quelli mostrati in figure 2 e 3. Dalla tabella 4 cediamo che in effetti Barbara è più precisa (ma di poco) rispetto ad Andrea, mentre Carlo è decisamente scarso.
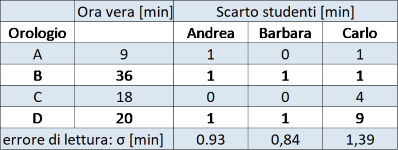
Le deviazioni standard calcolate rappresentano una stima dell’errore che Andrea, Barbara o Carlo fanno leggendo un orologio come quelli sopra. Bene, possiamo usare questi valori come la migliore stima dell’errore di lettura che essi avranno fatto leggendo poi l’orologio E in figura 4 e quindi preparare la tabella seguente:

Dovrebbe essere chiaro il significato di errore di lettura: dal momento che Barbara e Andrea sono più precisi di Carlo nella lettura, la riportano con un errore più piccolo, chi legge la tabella 5 sa che può fidarsi di più della lettura di Barbara che non di quella di Carlo.
Alcuni punti importanti
- Per valutare l’errore di lettura dell’orologio E in figura 4 abbiamo usato informazioni precedenti che ci hanno permesso di valutare l’abilità degli studenti nel leggere l’ora. Abbiamo poi usato questa informazione per assegnare un errore alla lettura dell’orologi E (figura 4). In questo caso l’errore riportato in tabella 5 è un errore di tipo B.
D.6: qui una discussione comune in classe sarebbe molto utile.
- Dal momento che la stima dell’errore è per sua natura una grandezza approssimata, non ha senso riportarne i valori con un numero di cifre significative maggiore di 2 (es. nel caso di Carlo σ=1.9365…. min). Alcuni prescrivono una cifra sugli errori di tipo B e due sugli errori di tipo A, altri suggeriscono di usare una seconda cifra qualora la prima sia 1 o 2. In ogni caso riportare due cifre significative (e un po’ di buon senso) sono generalmente precauzioni sufficienti.
- Esistono diversi formalismi per indicare l’errore, in tabella 5 ne sono mostrati due: indicare l’errore dopo il segno \(\pm\) è un modo, altrimenti si riporta tra parentesi l’errore sull’ultima cifra del dato (più conciso ma a volte meno chiaro).
- In alcuni casi si trascura l’indicazione dell’errore (cosa fortemente sconsigliata) lasciando all’intuito del lettore il compito di capire la precisione che vogliamo dare al valore che abbiamo letto (stiamo parlando di errori di lettura). In questi casi si sottintende che il numero di cifre significative rispecchia la nostra fiducia nel valore fornito. Quindi riportare x=1.2 vuol dire che siamo convinti di poter distinguere il valore letto da 1.3 o 1.4; scrivendo x=1.27 diciamo che siamo significativamente sicuri di poter distinguere il valore letto da 1.26 o 1.28; scrivendo x=1.275 siamo significativamente sicuri di poter distinguere il valore letto da 1.274 o 1.276, etc…E’ una prassi sconsigliata ma spesso usata soprattutto nella vita quotidiana.
Leggere tra le tacche
Verifichiamo ora la possibilità di leggere tra le divisioni della scala a seconda della propria abilità. Per questo utilizziamo un esperimento proposto nelle sue dispense dal Prof. G. D’Agostini (in particolare G. D’Agostini, Le basi del metodo sperimentale(1) cap.2, il pdf è riportato anche nelle schede).
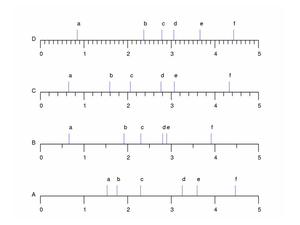
In figura 5 sono riportati 4 righelli in cui cambia la minima divisione della scala: \(\Delta x = 1,\ 0.5,\ 0.2,\ 0.1\) le immagini ad alta risoluzione sono nel file Fis-61.figureHR.pdf; si possono stampare e distribuire agli studenti. La figura 5 è stata realizzata usando il programma Gnuplot (freeware) con un semplice script che si può scaricare (vedi allegati) e modificare per cambiare scale e indici a proprio piacimento.
Si chiede agli studenti, dopo quanto detto sopra, di leggere con la precisione che ritengono opportuna la posizione dei 5 indici a-f sulle diverse scale e riportarli in una tabella. Attenzione: va letto ad occhio, senza usare altri strumenti di supporto. La tabella può essere importata in un foglio elettronico (vedi allegati) per il calcolo dell’errore di lettura. Anche se sarebbe utile stimolare gli studenti a calcolarlo loro stessi.
Nella prima pagina del foglio excel allegato si possono inserire i dati letti dallo studente. Nella seconda pagina il programma confronta i dati letti con i valori veri (inseriti in precedenza) calcolando gli scarti e la deviazione standard della distribuzione degli scarti.
In tabella 6 sono riportati i valori di riepilogo di due studenti (i files completi sono allegati).
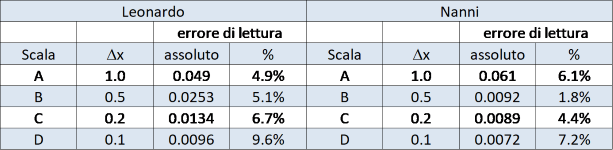
L’errore relativo è vicino a 1/20 della minor divisione della scala (ben lontano quindi dal
D.7: Usando i dati dell’esperimento proviamo ad associare un errore di lettura alla misura della figura 1 e confrontare l’errore di lettura stimato con l’incertezza che gli studenti avevano associato alla prima lettura.
Nota: Un esperimento analogo (vedi G. D’Agostini, Le basi del metodo sperimentale(1) cap.2) si può fare utilizzando un calibro a cursore o il calibro millimetrico presentato nell’articolo FIS-41 (Calibro Millimetrico): uno studente legge una misura senza utilizzare il nonio (ad esempio tenendolo coperto con nastro adesivo opaco) cercando di distinguere al meglio la posizione del cursore tra le tacche della scala. Quindi un secondo studente verifica la misura leggendo il nonio. Di quanto si discosta la lettura ad occhio?
Conclusioni
L’attività dovrebbe aver dimostrato che:
- L’errore di lettura è un errore di tipo B definito anche in base all’abilità dello sperimentatore, alla confidenza che egli ha nello strumento e alla fiducia nelle sue capacità.
- L’errore di lettura può essere determinato sperimentalmente misurando la capacità dell’osservatore di leggere tra le divisioni della scala.
- L’errore di lettura può essere tipicamente anche 1/10 della minima divisione della scala e, in condizioni ottimali, anche inferiore.
- Utilizzare 1/2 divisione come stima dell’errore è una pratica comoda ma sbagliata sia perchè sovrastima l’errore, sia dal punto di vista delle direttive del BIPM.
Domanda: uno strumento digitale con un display a 4 cifre mostra il valore X=12.34 [u.m.], quanto vale l’errore di lettura? In questo caso la risoluzione dello strumento è R=0.01[u.m.]. Lo strumento approssima con il valore X=12.34 [u.m.] tutti i valori:
ovvero:
R/2 rappresenta l’errore massimo sul valore letto, non l’errore di lettura. L’errore di lettura si calcola come la deviazione standard della distribuzione dei possibili risultati.
Per uno strumento digitale si assume una distribuzione uniforme dei valori letti all’interno dell’intervallo di risoluzione. La deviazione standard per una distribuzione uniforme in un intervallo di ampiezza R è:
quindi circa 1/3 dell’intervallo di risoluzione.
Note e storia
Note
1.: volendo ripetere l’esperimento degli orologi si possono preparare orologi analoghi a quelli usati infigura 2disegnando dei cerchi con il compasso e un lancetta in posizione casuale. Usiamo poi un goniometro per stabilire con precisione l’ora da confrontare con la lettura ad occhio.
2.: in effetti l’aspetto soggettivo degli errori di lettura si trova sottolineato di frequente:
A type of error associated with a directly measured quantity is called the “reading error”. […]: the person doing the measurement must guess how well he or she can read the instrument. A reasonable guess of the reading error of this micrometer might be 0.0002 cm on a good day. If the experimenter were up late the night before, the reading error might be 0.0005 cm.(Wolfram.com)
The reading error in a measurement indicates how accurately the scale can be read. In analogue readouts the reading error is usually taken as plus or minus half the smallest division on the scale, but can be one fifth (0.02) of the smallest division, depending on how accurately you think you can read the scale. In the end, it is down to your judgement. (nhn.nhn.ou.edu)
A rule of thumb for evaluating the reading error on analogue readout is to use half of the smallest division (i.e. in case of a meter stick with millimeter divisions it is 0.5 mm), but only the observer can ultimately decide what is his/her limitation in error evaluation(qui il documento completo)
Bibliografia
Nelle schede e allegati:
- Fis-61.rulers.plt: macro per il programma Gnuplot consente di generare un’immagine dei righelli di figura 5. Modificando la macro si possono cambiare scale e righelli.
- Fis-61.Ora.xls: foglio elettronico per trattare i dati della lettura degli orologi;
- Fis-61.rulers.xls: foglio elettronico per trattare i dati della lettura degli righelli;
- Fis-61.figureHR.pdf: immagini ad alta risoluzione da stampare e distribuire per riprodurre gli esperimenti.
Nelle relazioni:
- Fis-61.rulers_nome.xls (nome=carlo, nanni, leonardo) esempi di letture effettuate da diversi studenti.
Autori
Meneghini Carlo
Schede / Allegati
- Fis-61.rulers.xls
- Fis-61.Ora.xls
- Fis-61.FigureHR.pdf
- Fis-61.Dagostini.pdf
- Fis-61.GUM.pdf
- Fis-61.rulers.plt
Relazioni
Specifiche esperimentoMateria Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Uno o più strumenti di misura analogici Durata esperimento in classe 1 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Metodo sperimentale Teoria della misura Misure dirette Errore di lettura |