Riassunto / Abstract

L’esperimento prevede l’osservazione e la misurazione del tempo di caduta libera tramite la misurazione dell’accelerazione nel sistema di riferimento del corpo in caduta.

Scheda sintetica delle attività

1. Allestimento di un supporto per ottenere una caduta il più imperturbata possibile da un’altezza di almeno 5m;
2. preparazione di un contenitore che protegga lo smartphone e assicuri una caduta stabile e verticale;
3. misurazione online dell’accelerazione nel sistema di riferiemento dell’oggetto in caduta;
4. discussione del risultato offline;
5. misurazione del tempo di caduta.

Risorse necessarie

• Smartphone con app di presa dati (e.g. Sensor Kinetics PRO per Android);
• software di elaborazione dati (e.g. GeoGebra);
• aste, piedistalli e viti;
• filo di cotone o fibra sintetica;
• nastro adesivo;
• custodia di protezione per lo smartphone del tipo resistente all’acqua;
• peso di metallo;
• cordella metrica.

Prerequisiti necessari

• Concetti di posizione, velocità e accelerazione;
• concetto di sistema di riferimento inerziale e non inerziale;
• uso della app di acquisizione dati;
• uso del software di elaborazione dati.

Obiettivi di apprendimento

• Comprendere l’assenza di gravità (o, meglio, di microgravità) nei sistemi di riferimento in caduta libera;
• verificare la legge oraria del moto di caduta libera.

Dotazioni di sicurezza

Nessuna dotazione particolare.

Svolgimento

Criticità dell’esperimento

L’esperimento si propone di misurare l’accelerazione nel corso del moto di caduta di uno smartphone. Affinché la misura risulti sufficientemente accurata, occorre prestare attenzione ai seguenti aspetti:

• La caduta deve avere una durata sufficientemente lunga da poter permettere la misurazione dell’accelerazione in quel lasso di tempo;
• l’impatto dello smartphone deve essere attutito in modo da non provocare danni al dispositivo;
• la caduta deve partire nel modo più rapido possibile per minimizzare l’effetto di forze diverse dalla gravità che imprimano moti rotatori allo smartphone (e.g.: la mano dell’operatore);
• la caduta deve avvenire in modo che il dispositivo mantenga il più possibile lo stesso orientamento per tutta la durata della stessa.

Per ottenere una caduta di sufficiente durata, si è optato per fare cadere il dispositivo da una finestra situata al primo piano di un edificio scolastico in modo da avere una distanza da terra di circa 6 m, con un tempo previsto per la caduta di circa un secondo.

Previsioni teoriche

Lo spazio percorso durante la caduta può essere calcolato con la legge oraria del moto uniformemente accelerato.

A tal fine occorre conoscere il valore locale dell’accelerazione di gravità. La posizione geografica del punto in cui è stato condotto l’esperimento è stata determinata con il navigatore GPS integrato nello smartphone:

Latitudine: 44,287° EST Altitudine: 35 m s.l.m.

L’accelerazione di gravità locale è stata prelevata dal sito:
http://museo.liceofoscarini.it/virtuale/gravita.phtml?alt=35&lat=44.28&applica=calcola
e risulta essere \(g = 9,791\ m/s^2\).

Setup dell’esperimento

Con una cordella metrica si procede alla misurazione della distanza s fra il punto di partenza della caduta ed il punto di impatto; il valore misurato è: \(s = \left( 6,6 \pm 0,1 \right)\ m\).

L’errore attribuito a tale misura appare piuttosto grande ma tiene conto della difficoltà di stabilire con esattezza il punto di impatto e della difficoltà di tendere in posizione il più possibile verticale la cordella metrica.

Per attutire l’impatto si è fatto in modo che la caduta termini su un telo o su un largo cuscino. Vista la distanza, è difficile prevedere il luogo esatto dell’impatto, pertanto il telo o il cuscino dovranno coprire una zona piuttosto ampia.

Per minimizzare le forze che potrebbero disturbare la fase iniziale della caduta, si è predisposta una struttura alla quale legare lo smartphone (chiuso in una custodia di protezione) tramite un filo di cotone che viene tagliato all’inizio della caduta.

Riprodurre l’esperimento da un’altezza di caduta simile o superiore a quella proposta potrebbe comportare qualche problema nel caso non si disponga di una posizione in cui effettuare le operazioni necessarie, come ad esempio predisporre un telo sull’area di caduta. In tal caso si può prendere in considerazione l’idea di effettuare l’esperimento con un’altezza più breve, rimanendo in una stanza chiusa.

Si consiglia comunque di non scendere sotto i 2,0 m di altezza (corrispondente ad un tempo di caduta previsto di 0,6 s) onde evitare che il tempo di caduta risulti troppo breve e quindi soggetto a maggiori incertezze. Una minore altezza di caduta permette di predisporre un’area di impatto con il suolo di minori dimensioni, si potrebbe ad esempio preparare uno scatolone riempito con frammenti di polistirolo o gommapiuma.

Per ridurre la possibilità che lo smartphone ruoti e cambi posizione durante la caduta, si è provveduto ad appesantire la parte inferiore della custodia con un oggetto metallico in modo da abbassarne notevolmente la posizione del baricentro. 

Raccolta dei dati

Per prima cosa si installa sullo smartphone l’app per la raccolta dei dati dei sensori. Nel nostro caso è stata utilizzata la app “Sensor Kinetics PRO” su dispositivo Android.

Sono disponibili diverse frequenze di campionamento comprese fra 10 e 20 Hz. Si è scelto di operare con quella massima, pari a 20 Hz.

Se tramite l’applicazione di accede al grafico relativo all’accelerometro, vengono tracciati tre grafici, che corrispondono alle misure dell’accelerazione in funzione del tempo lungo i tre assi coordinati.

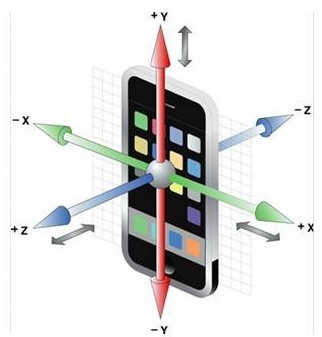
Se si appende lo smartphone al filo in modo che resti in posizione verticale il più possibile fermo, allora il grafico avrà un aspetto simile a quello in figura 3.

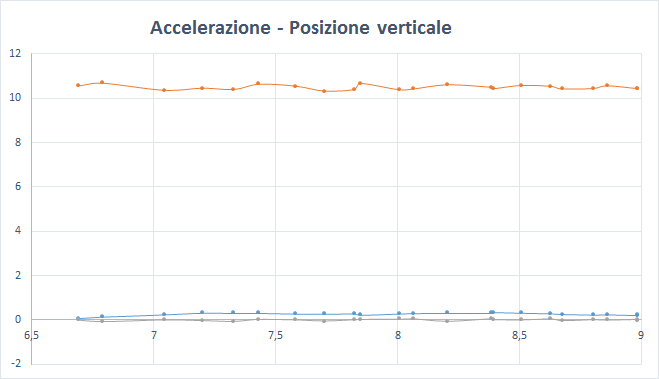
L’asse y, al quale corrisponde il grafico arancione, è quello in direzione verticale, corrispondente all’altezza dello smartphone. In una situazione di quiete registra l’accelerazione di gravità. Come si può notare, il dispositivo utilizzato misura un dato maggiore a quello previsto, Si provvederà in fase di analisi dei dati a dare una spiegazione e a correggere quello che si presenta come un errore sistematico.

Gli altri due assi riportano valori vicini allo zero, che possono essere considerati come “rumore”.

A questo punto si può procedere tagliando il filo e osservando la caduta del dispositivo, fino al momento in cui viene raccolto sul telo o sul cuscino al piano inferiore.

Quando la caduta sarà terminata, l’operatore al piano inferiore raccoglie lo smartphone, arresta la registrazione dei dati e salva gli stessi sul supporto elettronico.

Una volta salvati i dati e convertiti in un formato leggibile dal PC, si può procedere alla loro elaborazione con un foglio elettronico (MS Excel, Libre Office Calc).

Il risultato relativo alla fase di caduta è riportato nel grafico in figura 4.

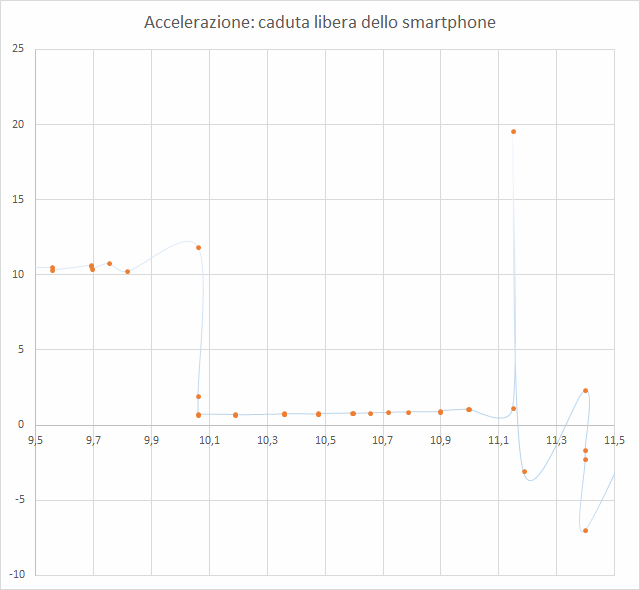
Analisi dei dati

Correzione di errori sistematici
Come evidenziato dal grafico in figura 2, l’accelerazione in posizione verticale è superiore a quella prevista. I primi istanti della caduta libera confermano che l’accelerazione lungo l’asse y non è nulla, come ci si può aspettare da un accelerometro in caduta libera, ma presenta un’accelerazione media di:

dove l’errore è stato assunto pari alla deviazione standard dei dati.
Sottraendo questo valore a quelli misurati dall’accelerometro nella fase in cui stazionava in posizione verticale si ottiene un dato medio di:

che rispecchia il valore atteso; anche in questo caso l’incertezza è rappresentata dalla deviazione standard.

Si conclude pertanto che l’accelerometro è soggetto ad un errore di taratura che inserisce nelle misure dell’accelerazione lungo l’asse y il bias indicato nella [1].

Analisi dell’accelerazione in fase di caduta libera

 Il grafico in figura 4 ci permette di notare che la caduta è sicuramente avvenuta nell’intervallo di tempo compreso fra 9,7 s e 11,2 s. Possiamo pertanto concentrare su questi dati l’analisi. Tabella 1 riporta i dati prelevati dall’accelerometro in quell’intervallo di tempo:

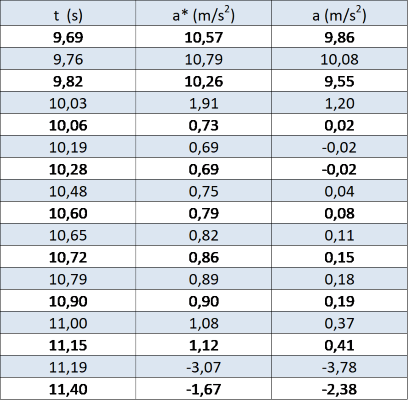
Si può evincere dai dati della tabella che la caduta è iniziata al tempo:

Il tempo riportato si ottiene eseguendo la media aritmetica fra l’ultimo tempo misurato in cui l’accelerazione era vicina al valore dell’accelerazione di gravità ed il primo in cui è vicina a zero. L’incertezza riportata è legata alla frequenza di campionamento dello smartphone.

Come si può notare dal brusco cambiamento nel valore dell’accelerazione lungo l’asse z. Da questo punto in avanti tutti i grafici relativi all’accelerazione riportano valori vicini allo zero.

Nella fase di caduta lo smartphone si trova in un sistema di riferimento in cui l’accelerazione di gravità è compensata dall’accelerazione del sistema, pertanto si viene a trovare in una situazione di assenza apparente di gravità, come dimostrano i valori pressoché nulli registrati dall’accelerometro.

Il termine della caduta avviene in corrispondenza del tempo

dove si registra una brusca accelerazione che coinvolge tutte le direzioni. È l’accelerazione dovuta all’impatto dello smartphone con il telo o con il cuscino. Il modulo dell’accelerazione è poco significativo dal momento che dipende dal tipo di impatto con il telo. Le misure negli istanti successivi sono difficilmente interpretabili in quanto si riferiscono al moto disordinato del dispositivo nel telo e nel momento in cui viene raccolto dall’operatore.

Dai dati raccolti possiamo calcolare che il tempo impiegato per la caduta è:

\[\Delta t = t_2 – t_1 = \left( 1,15 \pm 0,07 \right)\ s\]

L’errore è ottenuto con la somma in quadratura degli errori assoluti.

Se si calcola con la legge del moto uniformemente accelerato lo spazio percorso in tale tempo si ottiene il valore di:

Si è ottenuto l’errore sommando in quadratura gli errori relativi. 
Tale valore è compatibile entro gli errori di misura con quello misurato tramite la cordella metrica di \(\left( 6,6 \pm 0,1 \right)\ m\).

Considerazioni sulle misure di accelerazione

Dalla Tabella 1 si può notare che i valori dell’accelerazione misurati nella fase di caduta evidenziano una tendenza all’aumento. Riportiamo i dati su un grafico, riportato in figura 5.

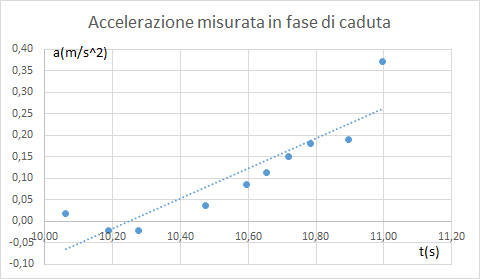
Visto l’andamento crescente, ipotizziamo un andamento lineare e calcoliamo la retta\(a = m \cdot t +b\) di miglior adattamento.
Si ottiene così la retta:

dove i coefficienti \(m\) e \(b\) e le relative incertezze sono:

Il coefficiente di correlazione R = 0,803 testimonia un certo accordo fra i dati ed il fit lineare.

La variazione lineare dell’accelerazione può essere dovuta a due fattori:

• una rotazione dell’asse dello smartphone durante la caduta;
• l’effetto dell’attrito viscoso dell’aria sullo smartphone.

 La prima ipotesi può essere verificata calcolando il modulo della somma vettoriale di tutte e tre le componenti dell’accelerazione misurate. Tale modulo rimarrebbe costante se la crescita osservata fosse imputabile ad una rotazione.

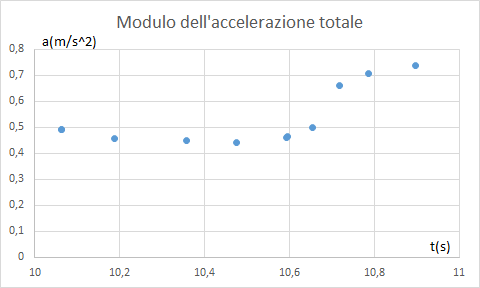
Nonostante si registri un valore sostanzialmente costante nella prima fase della caduta, è evidente una crescita del modulo nella seconda parte che induce a pensare che non sia una eventuale rotazione a spiegare l’incremento di accelerazione lungo l’asse y.

Imputiamo allora all’attrito viscoso dell’aria l’accelerazione misurata; in questa ipotesi nel sistema di riferimento del laboratorio l’accelerazione di caduta è: 

e nel sistema di riferimento solidale con lo smartphone è:

La costante di tempo del fenomeno è \(\tau = \large{\frac{m}{\beta}}\), dove β è il coefficiente di proporzionalità tra la forza di resistenza viscosa dovuta all’aria e la velocità dello smartphone \(F_v = -\beta v\); essendo β molto piccolo, \(\tau\) è molto grande e pertanto il rapporto \(t/\tau\) è molto piccolo per tutti i valori di \(t\) dell’esperimento. Ricordando che per piccole \(x\) l’esponenziale \(e^x \simeq 1 + x\), possiamo quindi approssimare a’ con:

il modello prevede quindi una crescita lineare dell’accelerazione misurata dallo smartphone in caduta libera, in accordo con l’esperimento;  nel nostro caso \(m\) vale 0,35.

Per valutare l’effetto di questo termine, calcoliamo l’equazione oraria s(t), considerando che l’ accelerazione di caduta non è costante e pari a \(g = 9,80 m/s^2\) come previsto dalla [2],  bensì: \(ge^{-t/\tau} \simeq g-mt\). Integriamo due volte questa accelerazione rispetto al tempo per ottenere la legge oraria del moto, che non sarà più quella del moto uniformemente accelerato, ma comprenderà anche un termine cubico; infatti:

che differisce dalla [3] per il termine \(-\large{\frac{1}{6}}mt^3\) .
Valutiamo l’effetto di questo termine al tempo di caduta pari a 1,25 s; risulta:

La correzione da apportare alla [3] risulta pertanto abbondantemente assorbita dall’incertezza riportata nella [3] stessa, che risulta 10 volte maggiore.

Note e storia

L’esperimento fa parte del progetto “Science Smart Kit”. Tale progetto comprende un kit di “accessori” per smartphone per realizzare attività di laboratorio di fisica, di scienze, chimica e matematica, schede per studenti e docenti, e la disseminazione attraverso iniziative di aggiornamento e formazione docenti.

Il progetto è risultato tra i vincitori del bando del MIUR “Nuove idee per la didattica laboratoriale nei Licei Scientifici”.

Bibliografia

• Patrik Vogt, Jochen Kuhn, “Analyzing free fall with a smartphone acceleration sensor”, The Physics Teacher, Vol. 50, 182, March 2012 tradotto in La Fisica nella scuola, XLVI, 2, 2013.

Autori

Seganti Alessio

 

Specifiche esperimento Materia Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Strumentazione semplice Reperibilità del materiale Uso quotidiano Materiale specifico Aste, piedistalli e viti, custodia di protezione per lo smartphone, peso di metallo, cordella metrica Durata esperimento in classe 2 h Capacità di bricolage/assemblaggio Sì Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone Sì Parole chiave Meccanica Dinamica del punto materiale Accelerometro Moto di un grave