Riassunto / Abstract

Si propone un antico esperimento didattico per verificare la II legge della Dinamica con un sistema formato da una carrucola e due masse (macchina di Atwood).
La macchina di Atwood è un sistema molto interessante e relativamente semplice da realizzare, tramite il quale si può controllare l’accelerazione scegliendo opportunamente le masse appese. In questo modo si possono realizzare moti di caduta abbastanza “lenti” da poter essere valutati senza l’uso di strumentazione sofisticata e senza dover trattare l’attrito con l’aria, non trascurabile se la velocità diventa elevata.

Scheda sintetica delle attività

Generalmente la II legge della Dinamica si introduce sperimentalmente e con successo utilizzando la rotaia a cuscino d’aria. Volendo proporre una prova che gli alunni possano gestire da soli, si potrebbero utilizzare carrelli in moto su di un tavolo. Tuttavia l’attrito con il piano non è facile da trattare a meno di non appesantire molto la prova. Con una carrucola a basso attrito, invece, utilizzando l’assetto della “macchina di Atwood”, si può fare (figura 1).

Figura 1: apparato sperimentale alla “Atwood”

La prova si presta ad utili approfondimenti: dalla misura di g, alla conservazione dell’energia.

Risorse necessarie

Asta lunga 70-80 cm;
morsa da tavolo;
morsetto con perno;
carrucola a basso attrito;
pesiera completa da 100g e 2 da 250g, qualche pesino da 1g (sostituibile con rondelle);
filo di cotone;
cronometro e metro.

Prerequisiti necessari

Saper fare misure di tempo e di spazio;
conoscere la legge del moto uniformemente accelerato;
conoscere la relazione tra grandezze direttamente e inversamente proporzionali.

Obiettivi di apprendimento

Saper discutere l’effetto della forza sul sistema mettendolo in relazione al moto;
saper argomentare riguardo alla massa nella Dinamica di un sistema composto;
verificare la II Legge della Dinamica.

Dotazioni di sicurezza

Nessuna

Svolgimento

Premessa

Conviene introdurre la prova lavorando in condizioni di equilibrio ossia ponendo le stesse masse ai capi del filo osservando che il sistema è in equilibrio qualunque sia la posizione delle masse stesse. Generalmente si parte con una pesiera da 100g completa per parte. Tirando leggermente una delle due masse si osserva qualitativamente che il moto del sistema è rettilineo uniforme (velocità costante). Il passo successivo è di considerare masse diverse osservando qualitativamente come si muove il sistema. A questo punto si invitano i ragazzi a proporre la metodologia da seguire per effettuare la misura dell’accelerazione del moto mantenendo la massa costante.

ATTENZIONE: Non è agevole verificare sperimentalmente che il moto è uniformemente accelerato poiché non si riesce a completare un set di almeno 5-6 misure di caduta con spazi diversi. Occorrerebbe un’asta molto più lunga. Gli alunni di solito propongono spontaneamente l’ipotesi che il moto sia uniformemente accelerato perché comunque le forze in gioco sono costanti.

Normalmente gli alunni, avendo già visto la prova con la rotaia a cuscino d’aria, rispondono correttamente che si devono spostare i pesini da una pesiera all’altra.

Se invece si vuole mantenere la forza costante, si variano le masse delle pesiere, lasciando invariata la loro differenza.

La difficoltà della prova consiste nel trovare l’assetto giusto per poter fare delle misure affette da errori contenuti, per fare ciò occorrono masse “grandi”, ma forze (determinate dalle differenze delle masse) “piccole”; da numerose prove effettuate si evince che con massa totale attorno ai 400g e differenze attorno ai 20g (massimo), il moto ha un’accelerazione stimabile misurando “a mano” tempo e spazio con errori contenuti.

ATTENZIONE a considerare differenze di massa troppo piccole (dell’ordine del grammo), le forze in gioco potrebbero essere confrontabili con gli attriti e portare a risultati di difficile interpretazione.

Ripetere le misure di tempo almeno 5 volte (facendo la media e calcolando la deviazione standard), con distanze di caduta attorno ai 50 cm, ma non inferiori ai 30cm.

Spesso gli alunni non riescono subito a capire quali masse e distanze considerare e ciò innesca utili discussioni tra loro e con l’insegnante.

Introduzione teorica

Lo schema di una macchina di Atwood con il diagramma di corpo libero è il seguente:

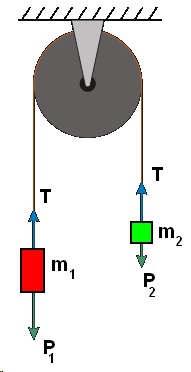
Applicando la II legge della Dinamica alle masse \(m_1\) ed \(m_2\) si ottiene:

\[\begin{array}{rl} P_1 – T = m_1 a \\ T – P_2 = m_2 a \end{array}\]

Sommando membro a membro si ottiene:

\[F_{tot} = P_1 – P_2 = \left( m_1 + m_2 \right) a = M_{tot} a\ \ \ \ \ \ [1]\]

Se \(m_1>m_2\) , la posizione iniziale sarà con \(m_1\) in alto e \(m_2\) a contatto del banco.
Se \(h\) è la distanza dal fondo della pesiera \(m_1\) al banco e \(t_m\) è la media dei tempi misurati di caduta di \(m_1\), dalla legge oraria del moto uniformemente accelerato si può calcolare l’accelerazione del sistema con la relazione:

\[a = \frac{2h}{t_m^2}\]

Come approfondimento notiamo che dalla [1] si può determinare \(g\); infatti:

\[P_1 – P_2 = \left(m_1 – m_2 \right)g = M_{tot} a \hspace{5 mm} \Longrightarrow \hspace{5 mm} g = \frac{m_1 + m_2}{m_1 – m_2} \cdot a\]

Per verificare la reazione [1] usiamo due strategie diverse.

I parte: Verifichiamo che la forza totale è direttamente proporzionale all’accelerazione

Variamo \(m_1\) ed \(m_2\) mantenendo costante la loro somma \(M_{tot}\) per almeno 5 serie di misure. Determiniamo poi la costante di proporzionalità tra la forza e l’accelerazione, confrondola con il valore atteso \(M_{tot}\) .

Facciamo poi il grafico di \(F_{tot}\ vs\ a\), ricavando la retta di interpolazione.

II parte: Verifichiamo che la massa totale è inversamente proporzionale all’accelerazione

Variamo \(m_1\) ed \(m_2\) mantenendo costante la loro differenza per almeno 5 serie di misure. Determiniamo poi la costante di proporzionalità tra la massa e l’accelerazione, confrontandola con il valore atteso \(F_{tot}\).

Facciamo poi il grafico di \(M_{tot}\ vs\ 1/a\), ricavando la retta di interpolazione.

In allegato il file per la raccolta dati con foglio elettronico.

Esempio di dati raccolti

errore su \(h=0,1cm\);
errore su \(t=0,1s\);
errore su \(m=1g\);
errore su \(M_{tot} =1,4g\).

Il tempo \(t_m\) è ricavato ripetendo la misura 5 volte.

L’errore sulla distanza è preso pari alla sensibilità dello strumento, probabilmente è un po’ sottostimato considerando che il metro potrebbe essere leggermente inclinato.

Vengono presi in considerazione i valori nominali delle masse. Alcune pesiere complete (a caso) sono state pesate sulla bilancia elettronica e raramente la misura si discostava dal valore nominale per più di 1g. E’ sembrato dunque ragionevole considerare questo come errore delle masse.

L’errore sulle misure di tempo è confrontabile con il tempo di reazione, l’errore sulla media è dato dalla:

\[e_m = \frac{ \sigma}{\sqrt{n}}\]

dove n è il numero delle misure.
L’errore della massa totale e della differenza delle masse è calcolato in quadratura. Tutti gli altri errori sono calcolati con le usuali regole di propagazione.

Risultati I parte

Tabella 1 riporta i dati sperimentali e la elaborazione per la I parte dell’esperimento

Tabella 1: dati sperimentali per la verifica della proporzionalità tra la forza totale e l’accelerazione; la costate di proporzionalità attesa è pari alla massa totale \(M_{tot}\)

La costante di proporzionalità media è (0,460±0,03)kg con un errore relativo dell’1%, in accordo con il valore atteso.

Risultati II parte

Tabella 2: dati sperimentali per la verifica della proporzionalità tra la massa totale \(M_{tot}\) e l’inverso della accelerazione misurata; la costante di proporzionalità attesa in questo caso è pari alla forza totale applicata

La costante di proporzionalità media è (0,189±0,01)N con un errore relativo del 3% e si discosta del 3,5% dal valore atteso.

Figura 1 riporta i grafici degli andamenti trovati nei due casi.

Figura 2: grafico della forza totale in funzione della accelerazione a massa totale costante (sinistra) e grafico della massa totale in funzione dell’inverso della accelerazione a forza totale costante (destra)

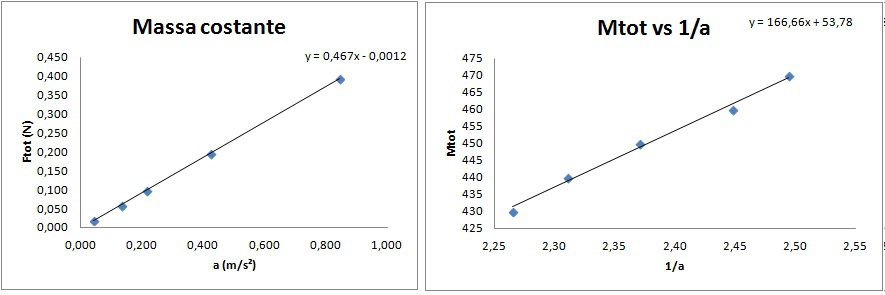
Notiamo che se consideriamo il coefficiente angolare delle rette di interpolazione riportati sui grafici, i risultati sono leggermente diversi e si discostano dal valore atteso del 1,5% nel primo caso e del 15% nel secondo.

In allegato altre misure (molto meno accurate) di gruppi di lavoro diversi.

Per aiutare la rielaborazione si possono proporre le seguenti domande:

Qual è la “massa” nei nostri esperimenti?
Quale relazione sussiste tra la forza applicata e l’accelerazione prodotta? Da cosa si ricava questa relazione? Come abbiamo proceduto operativamente per verificarla?
Quale relazione sussiste tra la massa e l’accelerazione? Da cosa si ricava questa relazione? Come abbiamo proceduto operativamente per verificarla?
Potresti realizzare un esperimento con la macchina di Atwood in cui l’accelerazione si mantenga costante pur variando la forza applicata e la massa? Argomenta anche riportando dei valori numerici.
Quali sono le maggiori fonti di errore?
Scrivi la relazione tra \(F_{tot},\ M_{tot}\ ed\ a\) che riesce a descrivere tutti questi esperimenti indicando anche le unità di misura delle grandezze nel S.I.. Come si chiama questa relazione?

Approfondimento

Potrebbe essere necessario tener conto del momento di inerzia della carrucola; è certamente utile discutere l’effetto del momento di inerzia della carrucola potrebbe essere utile per approfondire l’argomento quando si vanno a trattare i moti dei corpi estesi.

Note e storia

La macchina di Atwood fu progettata nel 1786 da George Atwood, matematico e fisico (e scacchista) inglese per poter condurre esperimenti di cinematica e dinamica con cui illustrare le sue lezioni di Fisica.

Bibliografia

http://it.wikipedia.org/wiki/Macchina_di_Atwood;
Per una trattazione della macchina di Atwood con sistema di acquisizione dati on line: B.Pecori, G.Torzo, A.Sconza: Come valorizzare un antico esperimento didattico con la tecnica MBL: La macchina di Atwood per condurre una ricerca sperimentale sul moto; in La fisica nella Scuola, XXXI, 1998 pag 83.

Autori

Arvati Susanna

Schede / Allegati

F=ma_con_Atwood

Relazioni

Specifiche esperimento

Materia
Fisica
Classi a cui è rivolto
2° biennio
Tipologia di laboratorio
Povero
Reperibilità del materiale
Uso quotidiano, negozi specializzati, siti web
Materiale specifico
Asta, carrucola, metro, cronometro, pesi vari
Durata esperimento in classe
3 h
Capacità di bricolage/assemblaggio
Sì
Necessità lavorazioni meccaniche/elettroniche
No
Necessità PC per acqusizione/analisi dati
No
Necessità di uno smartphone
No
Parole chiave
Meccanica
Dinamica del punto materiale
Moto uniformemente accelerato
Meccanica dei sistemi