Riassunto / Abstract

Si propone una esperienza per verificare sperimentalmente uno dei più importanti e noti principi di conservazione della Fisica, quello dell’energia meccanica, attraverso la sola misurazione di tre lunghezze, con l’esclusivo impiego di materiale di facile reperibilità e di costo irrisorio, che tuttavia coinvolge aspetti teorici fondamentali che vanno dal moto parabolico alla dinamica rotazionale del corpo rigido.

L’attività è consigliata per le classi terze ed è eseguibile, oltre che in laboratorio, anche individualmente a casa o, in piccoli gruppi, in aula.

Scheda sintetica delle attività

Si richiamano le nozioni fondamentali di energia potenziale gravitazionale U e di energia cinetica K del punto materiale in moto lungo una guida inclinata e l’enunciato del principio di conservazione dell’energia meccanica.
Al fine di verificare l’uguaglianza U=K si discute la modalità di misurazione della velocità nel punto più basso della guida ed eventualmente si suggerisce, allo scopo, di sfruttare le conoscenze di cinematica del moto parabolico che all’occorrenza vengono richiamate.
Per semplificare calcoli e misurazioni si sottolinea l’utilità di far si che l’ultimo tratto, più basso, della guida sia in piano, assicurandosi, così, che la velocità della sferetta al distacco dalla guida abbia solo componente orizzontale.
Se dovessero emergere perplessità circa gli effetti derivanti dalla forma della guida (non esattamente equivalente ad un piano inclinato) si richiama la natura conservativa della forza gravitazionale.
Si esegue l’esperienza e si discutono i risultati, ottenuti in approssimazione di punto materiale, che mostrano evidenti differenze con le aspettative teoriche.
Eventualmente non emerga spontaneamente, si fa osservare che il modello teorico del punto materiale non è applicabile all’esperienza in questione e, rimarcando la natura estesa della sferetta, si richiamano le nozioni della dinamica del corpo rigido e dell’energia cinetica rotazionale in particolare nel caso del rotolamento senza strisciamento.
Si ripete l’esperienza cercando di garantire la condizione di non slittamento, senza cioè elevare eccessivamente la quota di partenza della sferetta1.
Si discutono i risultati ottenuti dai diversi gruppi con diverse sferette e diverse guide.

Risorse necessarie

Guida semirigida (di PVC, alluminio, rame) di lunghezze tra 60cm e 80cm;
sferetta di acciaio (Geomag) , sferetta di gomma (è adatta la sferetta di un vecchio mouse);
foglio di carta possibilmente a quadretti;
foglio di carta carbone;
nastro biadesivo;
supporto di sostegno con aste e morsetto (sostituibili con un qualunque supporto di sostegno per sollevare un estremo della guida, per lo svolgimento a casa o in aula);
filo a piombo;
righello, squadretta o metro a nastro;
bilancia (opzionale);
forbici.

Figura 1: materiale necessario per l’esperimento

Prerequisiti necessari

Nozioni di cinematica e di dinamica;
nozioni di calcolo degli errori sperimentali;
saper usare, eventualmente, un foglio elettronico per l’elaborazione dei dati.

Obiettivi di apprendimento

Saper progettare e realizzare un’esperienza;
Capire l’importanza della teoria nella pratica;
Saper valutare le incertezze sperimentali;
Saper lavorare in gruppo nell’allestimento dell’esperienza, nella sua esecuzione e nella valutazione critica dei risultati ottenuti.

Dotazioni di sicurezza

Nessuna

Svolgimento

Fase 1
Si allestisce l’apparato sperimentale come è schematizzato in figura 2

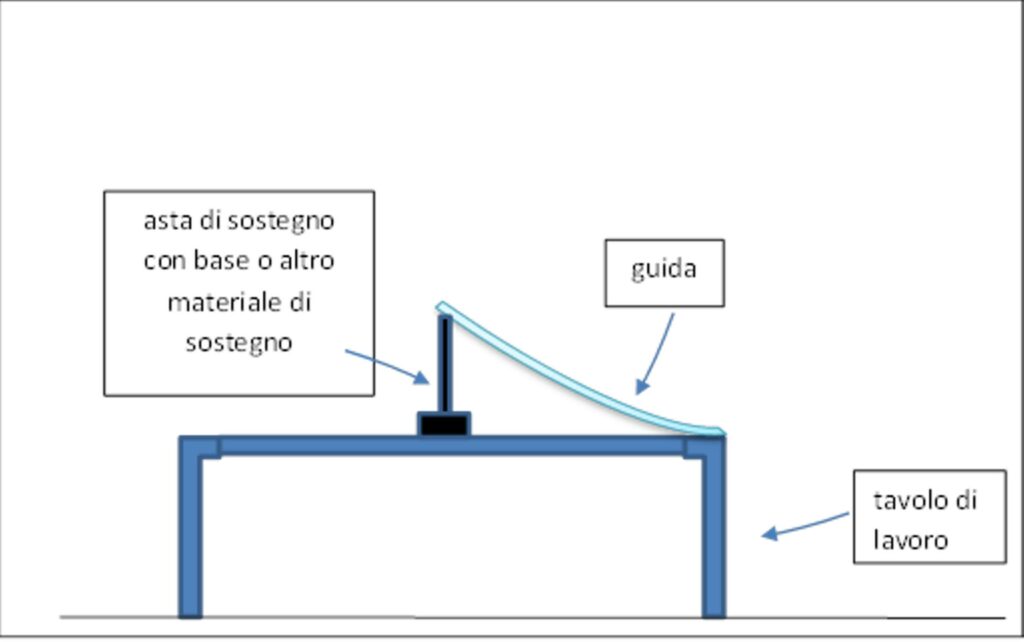
Si fissa la guida al bordo del tavolo di lavoro con del nastro biadesivo e, dalla parte opposta, la si tiene sollevata rispetto al tavolo con un supporto adeguato (possono andare bene, all’occorrenza, anche alcuni libri sovrapposti). Si deve evitare di elevare eccessivamente la guida per garantire per quanto possibile il rotolamento senza strisciamento (figura 3).

Figura 3: guida di rame fissata al tavolo e sostenuta dal supporto

Fase 2

Con il nastro biadesivo, si fissa al pavimento, di fronte alla guida, un foglio di carta e al di sopra di questo un foglio di carta carbone (figura 4); per capire dove sia meglio posizionare il foglio di carta è bene fare alcune prove di caduta della sferetta.

Figura 4: posizionamento del foglio di carta sul pavimento e foglio di carta carbone

Fase 3. Si utilizza il filo a piombo per determinare due punti sul pavimento al di sotto dell’estremità della guida al bordo del tavolo e si traccia una linea sul pavimento passante per detti punti

Fase 4. Si contrassegnano sulla guida almeno tre punti, distanti due/tre cm l’uno dall’altro, a partire dal punto più alto della guida. Verranno utilizzati per ripetere l’esperienza facendo partire la sferetta da quote diverse.

Fase 5. Si misurano direttamente la massa \(m\) della sferetta, l’altezza \(h_1\) di rilascio rispetto al piano del tavolo, l’altezza \(h_2\) del piano del tavolo rispetto al pavimento (figura 5)

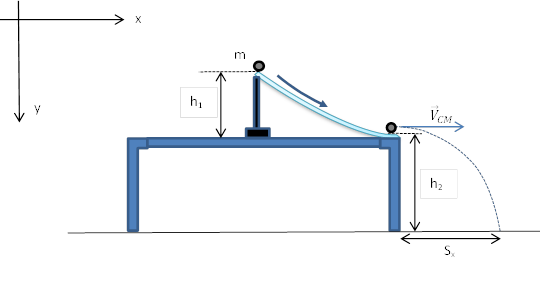
Figura 5: schema dell’esperimento con l’identificazione delle grandezze da misurare

Fase 6. Si posiziona la sferetta nel punto più alto contrassegnato sulla guida e la si lascia andare. Cadendo sul foglio di carta carbone essa lascerà un segno sul foglio di carta. Si misura la distanza \(S_x\) dalla verticale dal bordo del tavolo al punto di caduta.

Fase 7. Si ripete per altre due volte la fase 6 e si mediano i valori di \(S_x\) trovati. E’ bene numerare progressivamente i segni impressi dalla sferetta sul foglio.

Fase 8. Poiché la velocità della sferetta nel momento in cui inizia la caduta libera è data da (vedere nota 3):

\[V = S_x \sqrt{\frac{g}{2h_2}}\ \ \ \ \ \ [1]\]

volendo verificare l’uguaglianza tra l’energia potenziale gravitazionale iniziale \(U_1\) e l’energia cinetica \(K_2\) alla base della guida \(U_1=K_2\) ovvero deve risultare \(mgh_1 = \frac{1}{2}mV^2\).
Ricavando V e sostituendo nella relazione [1], si ottiene:

\[S_x = 2 \sqrt{h_1h_2}\ \ \ \ \ \ [2]\]

In altre parole la verifica del principio di conservazione si ridurrebbe alla verifica dell’uguaglianza [2].

Fase 9. Si registrano i valori misurati di \(S_x\) con le rispettive incertezze e si calcolano i valori attesi per \(S_x\) in base alla relazione [2]; gli errori sulle grandezze misurate direttamente sono assunti uguali alla sensibilità strumentale, gli errori sulle grandezze derivate sono calcolati mediante la propagazione degli errori.

I dati sperimentali possono essere elaborati mediante un foglio elettronico predisposto allo scopo (vedi allegato: elabor_senza_rot).

Un esempio di dati sperimentali ottenuti è il seguente:

Materiale della guida: rame;
dimensioni della guida: 75,9cm x 0,5cm x 0,05cm;
sferetta di gomma: massa= (27±1)g, diametro= (2,13±0,05)cm.

Tabella 1: valori misurati di \(h_1\), \(h_2\) e \(S_x\) e valori attesi di \(S_x\) in base alla relazione [2]

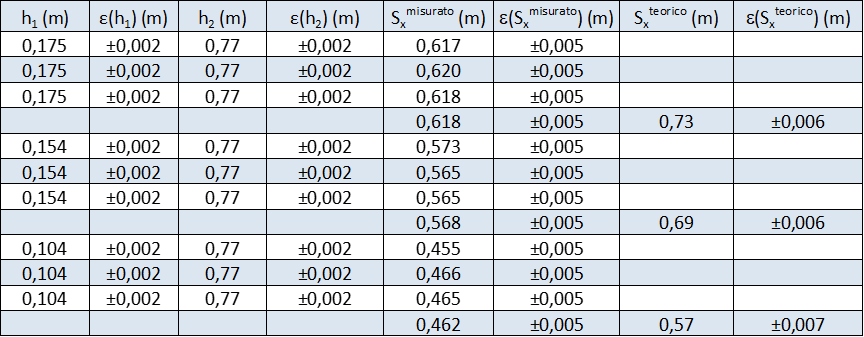
Notare come i valori attesi e i valori sperimentali di \(S_x\), non siano in accordo tra di loro; i valori misurati risultano inferiori ai valori attesi, presumibilmente a seguito di una perdita di energia cinetica durante il moto lungo la guida.

Per una verifica supplementare si è riportata anche una tabella con i valori dell’energia potenziale in cima alla guida (U) e dell’energia cinetica di pura traslazione in fondo alla guida K ottenuti con i dati a disposizione (vedi file excel allegato elabor_senza_rot).

Tabella 2: confronto tra i valori dell’energia potenziale iniziale U e dell’energia cinetica finale K calcolata utilizzando il valore misurato della velocità.

Come si può vedere c’è discrepanza tra U (in cima alla guida) e K di circa 0.01(J). In particolare si nota come i valori osservati dell’energia potenziale siano sempre leggermente maggiori di quelli dell’energia cinetica. Ciò conferma una “perdita” di energia, qualitativamente in accordo con i valori misurati della gittata tutti inferiori ai valori attesi.

Viste le dimensioni della sferetta si può non attribuire tale “perdita” alla resistenza dell’aria (sia nella fase di moto sulla guida che in quella di caduta libera) che si può ragionevolmente ritenere trascurabile.

Fase 10. Si richiama l’attenzione sul fatto che la sferetta non può approssimarsi ad un punto materiale in puro moto traslatorio ma che occorre tenere conto del suo moto di rotazione lungo la discesa e che parte della sua energia cinetica sia perciò di tipo rotazionale.
Prendendo in considerazione anche la rotazione della sferetta, l’energia cinetica complessiva, in assenza di strisciamento, è (vedere nota 4):

\[K_2 = \frac{7}{10}mv_{cm}^2\]

L’energia potenziale è sempre: \(U = mgh_1\); eguagliando i due termini abbiamo:

\[mgh_1 = \frac{7}{10}mv_{cm}^2 \longrightarrow h_1 = \frac{7}{10} \cdot \frac{S_x^2}{2h_2}\]

In definitiva, entro gli errori sperimentali, si va a verificare, la seguente relazione:

\[S_x = \sqrt{\frac{20}{7}h_1h_2}\ \ \ \ \ \ [3]\]

Fase 11. Si cambia la posizione di rilascio della sferetta secondo le quote prima stabilite e si ripetono le fasi precedenti.

I dati sperimentali possono essere elaborati mediante un foglio elettronico predisposto allo scopo (vedi allegato: elabor_con_rot):

Si riporta qui di seguito uno dei set di dati sperimentali ottenuti:

Materiale della guida: rame;
dimensioni della guida: 75,9cm x 10,5cm x 0,05cm;
sferetta di gomma: massa= (27±1)g, diametro= (2,13±0,05)cm.

Tabella 3: valori misurati di \(h_1\), \(h_2\) e \(S_x\) e valori attesi di \(S_x\) in base alla relazione {3}

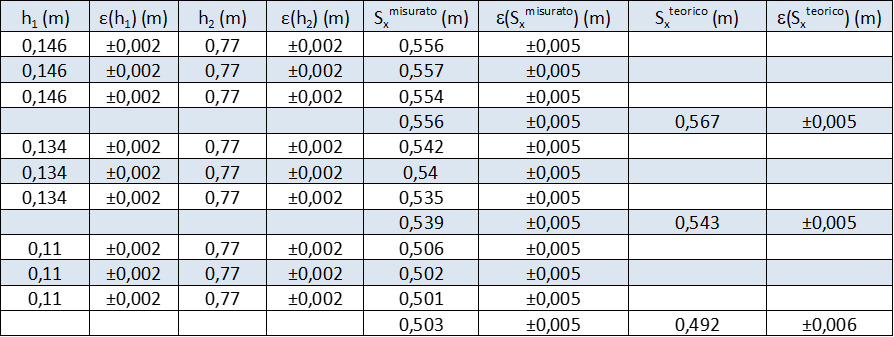
Ora i valori sperimentali di \(S_x\) sono in accordo con i valori attesi, entro l’incertezza della misura, confermando la validità del teorema di conservazione dell’energia cinetica.

Allo scopo di mettere maggiormente in risalto l’esito della verifica del principio di conservazione dell’energia si riportano anche i risultati ottenuti per l’energia potenziale e per l’energia cinetica (tabella 4):

Tabella 4: confronto tra i valori dell’energia potenziale iniziale U e dell’energia cinetica finale K calcolata utilizzando il valore misurato della velocità.

Notare come ora la differenza \(U – K\) è compatibile con lo zero entro gli errori di misura.

Fase 12. Si discutono i risultati sottolineando come nel moto di rototraslazione del corpo rigido una parte non trascurabile dell’energia cinetica sia sempre di tipo rotazionale e, a titolo d’esempio si può far vedere come uno yoyo si muove verso il basso più lentamente se, mentre cade, ruota, rispetto a quanto farebbe se dovesse semplicemente cadere.

I dati sperimentali riportati in precedenza riguardano il rotolamento di una sferetta di gomma su una guida di rame. Altri dati relativi al rotolamento della sferetta di gomma su una guida di alluminio e di una sferetta d’acciaio su guida di PVC sono riportati nel file Dati esperienza cons_energia presente tra gli allegati.

Negli allegati è possibile due fogli excel per l’elaborazione dei dati sperimentali e delle relative incertezze (il file elabor_senza_rot può essere utile per l’approccio in approssimazione di punto materiale, mentre se si tiene conto del rotolamento è utile il file elabor_con_rot).

Note e storia

Nota 1 Dalle prove effettuate, si è rilevato che i migliori risultati si ottengono con l’abbinamento sferetta mouse – guida di rame o alluminio e con sferetta d’acciaio – guida di PVC o di rame, con inclinazioni non superiori a 30°. Abbinamenti diversi o angolazioni maggiori sembrano non garantire il puro rotolamento.

Nota 2 La misurazione dell’altezza avviene tra il piano del tavolo e la quota alla quale si trova il punto di contatto della sferetta con la guida al momento del rilascio. A rigore andrebbe considerato il fatto che questo punto dista dalla quota del centro di massa della sferetta meno del suo raggio (figura 6).

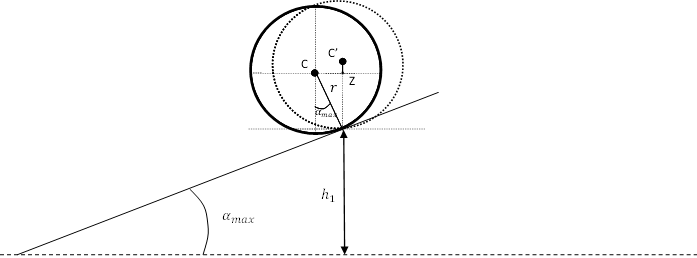
Figura 6: illustrazione della correzione da apportare alla altezza del centro della sferetta

La differenza C’Z è data da:

\[C’Z = r\left(1-cos \alpha_{max}\right)\]

dove \(\alpha_{max}\) è l’angolo di inclinazione della guida in prossimità del punto più alto di rilascio e che è normalmente maggiore degli angoli di inclinazione nei punti di rilascio a quota inferiore. Per angoli di inclinazione dell’ordine di 25° (quali sono quelli delle esperienze realizzate) si ha, per la sferetta di gomma e per quella d’acciaio:

\[\begin{array}{rl} r_{gomma} = 1,07\ cm \longrightarrow C’Z_{gomma} = r_{gomma}\left(1-cos \alpha_{max} \right) \simeq 0,001\ m \\ r_{acciaio} = 0,64\ cm \longrightarrow C’Z_{acciaio} = r_{gomma}\left(1-cos \alpha_{max} \right) \simeq 0,0006\ m \end{array}\]

Pertanto si è ritenuto trascurabile l’errore introdotto nel caso della sferetta d’acciaio mentre se ne è tenuto conto per la sferetta di gomma sottraendolo al valore di \(h_1\) misurato.

Nota 3 Dal momento in cui la sferetta abbandona la guida il suo moto è di tipo parabolico e, utilizzando il sistema di riferimento mostrato in figura 5 (assumendo l’origine nel punto di distacco dalla guida), è descritto dalle seguenti equazioni:

\[\begin{array}{rl} x(t) = V_{cm}t \ \ \ \ \ \ \longrightarrow S_x = V_{cm}t_{volo} \\ y(t) = \frac{1}{2}gt^2 \longrightarrow h_2 = \frac{1}{2}gt^2_{volo} \end{array}\]

dove \(t_{volo}\) è l’intervallo di tempo richiesto per la caduta libera. Eliminando \(t_{volo}\) dalle due precedenti equazioni si ottiene:

\[V_{cm} = S_x \sqrt{\frac{g}{2h_2}}\]

Nota 4 Sulla sommità della guida, ad un’altezza \(h_1\)dal tavolo di lavoro, la sferetta, di massa \(m\), rotola lungo la guida fino all’estremità opposta, al bordo del tavolo. Da questo punto, ad altezza \(h_2\) dal pavimento, la sferetta prosegue con moto parabolico fino a toccare il suolo a una distanza \(S_x\) dalla verticale condotta dal bordo del tavolo.

Dato che la sferetta inizia la discesa lungo la guida con velocità iniziale nulla si ha che l’energia cinetica iniziale \(K_1\) è nulla.
Detta \(U_1\) l’energia potenziale gravitazionale della sferetta ad inizio discesa rispetto al piano del tavolo e \(U_2\) l’energia potenziale a fine discesa si ha:

\[U_1 = mgh_1; \hspace{3 cm} U_2 = 0\]

Secondo il principio di conservazione dell’energia meccanica:

\[U_1 + K_1 = U_2 + K_2\]

dove \(K_2\) è l’energia cinetica a fine discesa.

La sferetta non scivola ma rotola lungo la guida e pertanto la sua energia cinetica è in ogni istante la somma di quella legata alla traslazione \(K_{tr}\) e di quella di rotazione \(K_{rot}\) la forza di attrito presente per garantire il non slittamento della sferetta, non compie lavoro dato che in ogni istante il punto di contatto della sferetta con la guida ha velocità relativa nulla, in assenza di strisciamento e considerate le ridotte dimensioni del corpo in rototraslazione).

Al termine della discesa l’energia cinetica sarà data dalla somma dei seguenti termini:

\[K_2 = K_{tr} + K_{rot} = {\frac{1}{2}mV_{cm}^2} + {\frac{1}{2}I \omega ^2}\]

dove con \(V_{cm}\) si intende la velocità del centro di massa della sferetta nel punto più basso della guida, con \(I\) il suo momento di inerzia rispetto ad un asse passante per il suo centro di massa e con \(\omega\) la sua velocità angolare di rotazione, al livello del tavolo, attorno a tale asse.
Sapendo che, in condizioni di puro rotolamento:

\[I = \frac{2}{5}mR^2; \hspace{3cm} \omega = \frac{V_{cm}}{R}\]

dove \(R\) è il raggio della sferetta, si ha:

\[K_{rot} = \frac{1}{2}I \omega^2 = \frac{1}{2} \left( \frac{2}{5}mR^2 \right) \left( \frac{V_{cm}}{R}\right)^2 = \frac{1}{5}mV_{cm}^2 \longrightarrow K_2 = \frac{1}{2} mV_{cm}^2 + \frac{1}{5} mV_{cm}^2 = \frac{7}{10} mV_{cm}^2\]

Nota 5 A rigore la misura della massa è ininfluente ai fini della verifica del principio di conservazione dell’energia, dato che allo scopo è sufficiente verificare l’uguaglianza [3] nella quale la massa non compare.

Bibliografia

http://www.webassign.net/labsgraceperiod/ncsulcpmech2/lab_4/manual.pdf (descrizione esperienza simile alla presente – in lingua inglese);
http://ssiscesto.altervista.org/pf_alessandra.pdf (sulla dinamica del punto materiale e del corpo rigido su piano inclinato; Scuola di Specializzazione all’Insegnamento Secondario “Raffaele La Porta” Sede dell’Aquila);
http://www.teachertube.com/viewVideo.php?video_id=28591&title=Energia_meccanica_e_conservazione (esperienza simile ma con apparecchiature da laboratorio di L. Battaia);
http://www.laboutloud.com/rampnroll/applet/applet.html (applet per lo studio del moto su profili ad inclinazione variabile);
https://phet.colorado.edu/sims/projectile-motion/projectile-motion_it.html (applet sul moto del proiettile);
https://phet.colorado.edu/it/simulation/energy-skate-park-basics (applet su scivolamento su profili curvi).

Autori

Pinna Franco

Schede / Allegati

Specifiche esperimento

Materia
Fisica
Classi a cui è rivolto
2° biennio
Tipologia di laboratorio
Povero
Reperibilità del materiale
Uso quotidiano, negozi specializzati, siti web
Materiale specifico
Guida semirigida, sferetta, bilancia
Durata esperimento in classe
1 h
Capacità di bricolage/assemblaggio
No
Necessità lavorazioni meccaniche/elettroniche
No
Necessità PC per acqusizione/analisi dati
No
Necessità di uno smartphone
No
Parole chiave
Meccanica
Dinamica del punto materiale
Conservazione dell’energia meccanica
Piano inclinato