Riassunto / Abstract

La legge di Lambert afferma che l’illuminamento I prodotto da una sorgente puntiforme che emette con un’intensità luminosa A in una certa direzione su una superficie piana perpendicolare alla direzione medesima è direttamente proporzionale al valore dell’intensità A e inversamente proporzionale al quadrato della distanza d tra la sorgente e la superficie considerata.
In questa esperienza si intende verificare tale legge limitatamente alla dipendenza dell’illuminamento in funzione della distanza reciproca tra sorgente e sensore (superficie illuminata).

Scheda sintetica delle attività

Si utilizza un binario metallico ad U (canalina) di un metro per costruire un rudimentale banco ottico; ad un estremo si fissa un sensore di luce e, facendo scivolare la torcia lungo il binario, si misura l’illuminamento I  misurato dal sensore per diverse posizioni della torcia. L’analisi dei dati misurati mostra che l’andamento misurato è in accordo con la legge di Lambert. Si osserverà anche che gli andamenti di I in funzione della distanza d tra la sorgente e il sensore  e in funzione di \(1/d^2\) sono in accordo con le previsioni della legge di Lambert.

Risorse necessarie

• Binario di metallo (1m);
• torcia;
• metro da sarta;
• sensore di luce;
• sistema di acquisizione on line  (si può utilizzare il sensore di luce dello smart-phone);
• pc con foglio elettronico;
• software di acquisizione dati (opzionale.

Prerequisiti necessari

• Saper utilizzare un foglio di calcolo;
• saper utilizzare programmi di acquisizione on line;
• saper riconoscere relazioni di proporzionalità diretta e inversa.

Obiettivi di apprendimento

• Riconoscere che l’illuminamento diminuisce con l’aumentare della distanza “d” dalla sorgente;
• determinare sperimentalmente la relazione funzionale fra le due grandezze caratteristiche del fenomeno;
• essere in grado interpretare grafici da cui desumere relazioni fra grandezze fisiche; 
• riconoscere che la legge esprime la conservazione dell’ energia.

Dotazioni di sicurezza

Nessuna

Svolgimento

Montare l’apparato sperimentale come mostrato in figura 1; limitare al massimo la luce ambiente e azzerare il sensore di luce in modo da evitare che vada in saturazione. Misurare l’illuminamento, per diverse distanze della sorgente ad intervalli di 5 cm; a titolo di esempio si riportano in tabella 1 i sperimentali dati ottenuti dagli studenti assieme i valori dell’inverso del quadrato della distanza d torciasensore e il prodotto dell’illuminamento misurato per il quadrato della distanza d. L’errore sull’illuminamento e sulla distanza d è pari alla sensibilità strumentale, quello su \(1/d^2\) e sul prodotto \(\textit{I} \cdot d^2\) è stato calcolato utilizzando la propagazione degli errori.

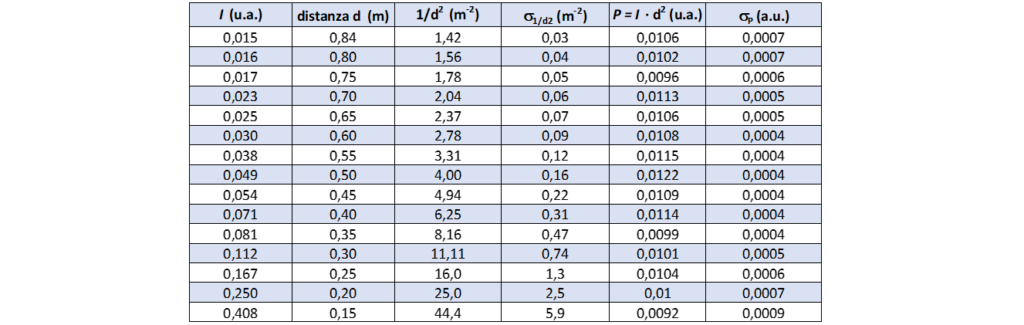
In base alla legge di Lambert il prodotto \(\textit{I} \cdot d^2\) dovrebbe essere costante, entro gli errori di misura. Calcolando il valore medio e la deviazione standard dei valori misurati otteniamo:

Concludiamo quindi che i valori sperimentali fluttuano tra di loro con una \(\sigma\) pari al 8% circa; con questo margine di incertezza, i valori sono tra di loro indistinguibili.

Figura 2 riporta il grafico dell’illuminamento in funzione della distanza d e la curva ottenuta dal fit dei dati sperimentali con un andamento \(1/d^2\)

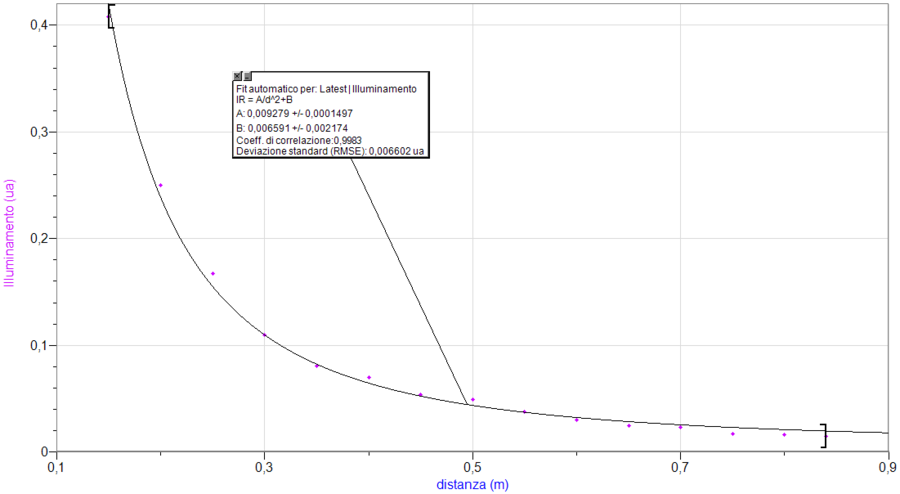
La curva di fit segue molto bene l’andamento previsto, a conferma della validità della legge di Lambert.

Una ulteriore conferma si ha dal grafico di figura 3, in cui è riportato l’andamento dell’illuminamento \(I\) in funzione di \(1/d^2\) che come previsto dalla legge di Lambert, presenta un andamento lineare.

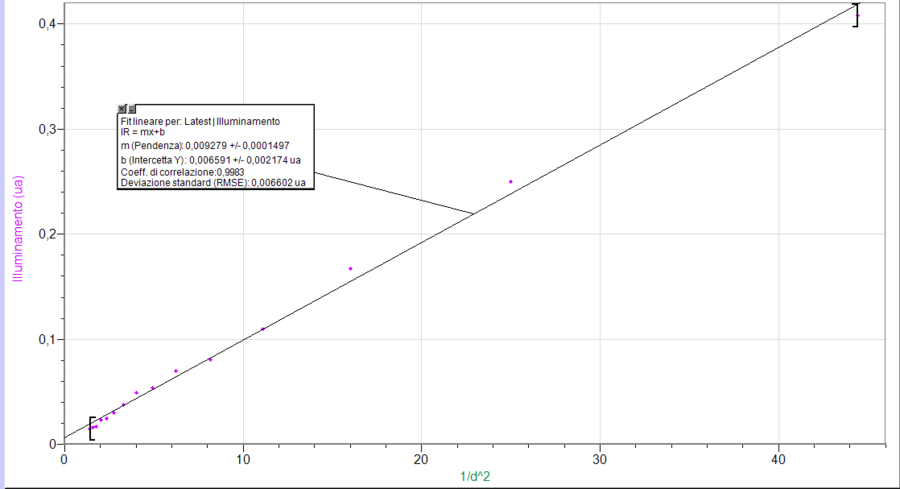
Note e storia

L’esperimento fa parte di una collezione di esperienze di laboratorio elaborate nell’ambito del  progetto  “Nuove idee per la didattica laboratoriale nei Licei Scientifici” finanziato dal MIUR

Autori

Diener Paola 
Ciardiello Eduardo 

Specifiche esperimento Materia Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Strumentazione semplice Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Guida metallica lineare, torcia, metro, sensore di luce Durata esperimento in classe 2 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Ottica Illuminamento Legge di Lambert Conservazione dell’energia