Riassunto / Abstract

Questo esperimento indaga la relazione tra energia assorbita ed energia emessa come fotoni in materiali semiconduttori, determinando il valore della costante di Plank.
L’esperienza permette anche di ricavare la caratteristica voltamperometrica di un LED e quindi determinarne la resistenza dinamica.

Scheda sintetica delle attività

Si misura la corrente che attraversa alcuni LED di colori diversi, polarizzati direttamente in funzione della differenza di potenziale applicata. Il comportamento non ohmico del diodo permette di individuare per ciascun colore una diversa tensione di soglia associata all’accensione del LED. 
Lo studio delle tensioni di soglia in funzione della lunghezza d’onda della luce emessa dai vari LED consente di ottenere una misura della costante di Planck. 

Risorse necessarie

• LED di diverse lunghezze d’onda; 
• generatore di tensione continua;
• multimetri analogici; 
• cavi di connessione; 
• basetta elettrica; 
• resistenza dal valore nominale di 220 Ω (tolleranza 5%).

Prerequisiti necessari

• Conoscere i meccanismi di conduzione elettrica; 
• saper effettuare misure di intensità di corrente e di tensione elettrica; 
• saper leggere la scala di un amperometro; 
• saper utilizzare le corrette unità di misura di corrente e differenza di potenziale; 
• conoscere il principio di conservazione dell’energia;
• conoscere la relazione di Einstein della energia di un fotone.

Obiettivi di apprendimento

• Indagare la relazione tra energia assorbita ed energia emessa in materiali semiconduttori; 
• indagare la relazione tra l’energia emessa e la frequenza dei fotoni emessi dal materiale.  

Dotazioni di sicurezza

Nessuna

Svolgimento

L’esperienza è divisibile in due parti. In una prima parte ci proponiamo di misurare le tensioni di soglia \(V_s\) di un certo numero di diodi-LED. Nella seconda parte invece si stima la costante di Planck sulla base delle misure prese precedentemente.

Parte I: Misura della tensione di soglia

Per alimentare i LED, si utilizza lo schema circuitale di figura 1, in cui i diodi sono polarizzati in modo diretto.

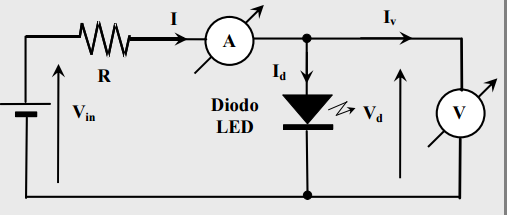
Per polarizzare direttamente un diodo occorre collegare  la giunzione p all’elettrodo positivo del generatore e quella n a quello negativo (figura 2).

Per individuare i due elettrodi del diodo, ricordiamo che per un LED il catodo  corrisponde alla struttura più corta e l’anodo a quella più lunga (figura 3).

La misura consiste nel misurare la differenza di potenziale ai capi del diodo \(\Delta V_{led}\) e la corrente che circola nel circuito, variando la tensione in ingresso \(\Delta V_{ingr}\).
Di seguito presentiamo i dati ottenuti per LED di colori diversi; le lunghezze d’onda indicate sono quelle riportate sui data-sheet dei led.

LED 1:  Giallo : \(\lambda = (600 \pm 22) nm\)

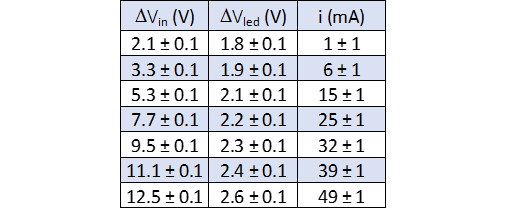
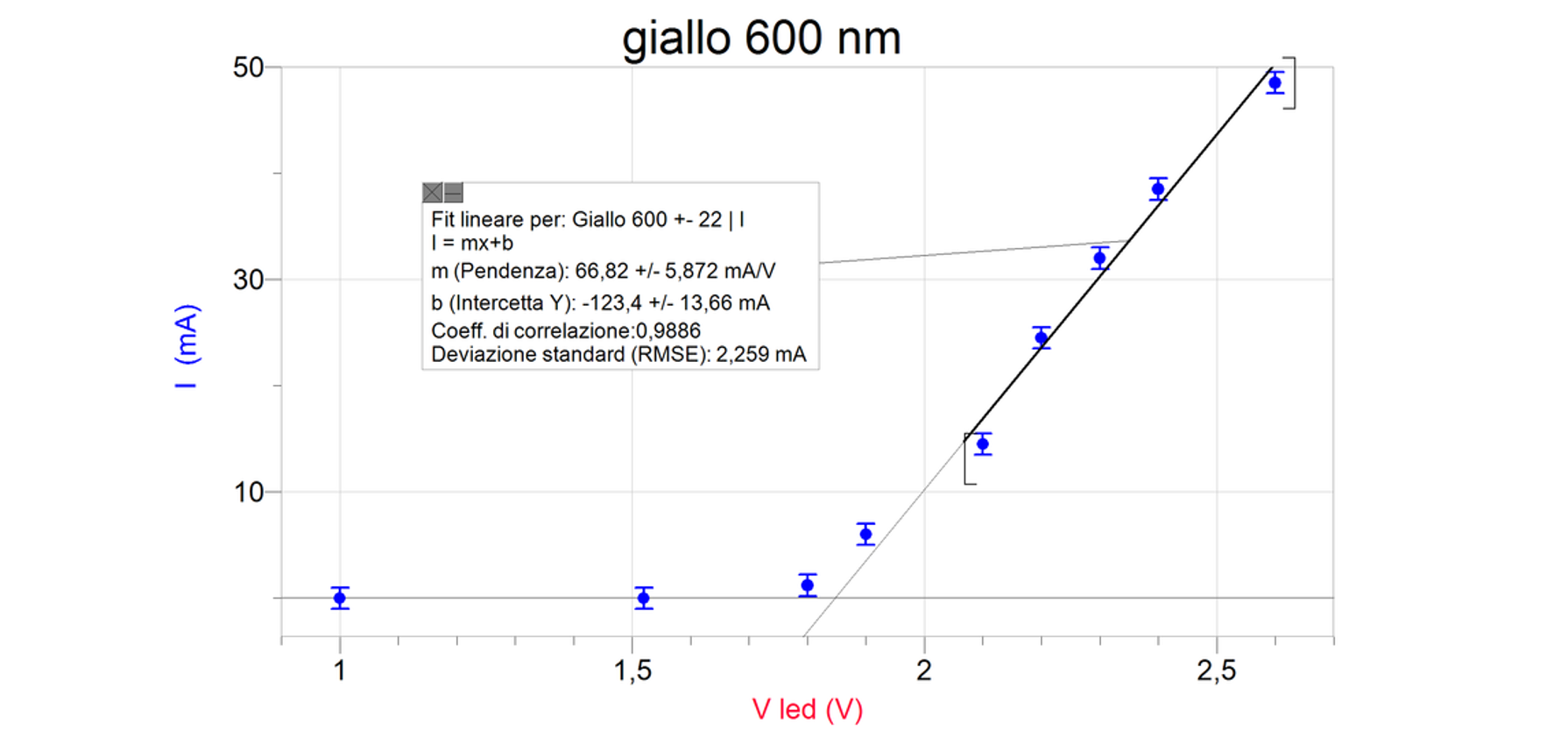
Dal grafico si nota che la corrente nel diodo è molto piccola per valori \(V_{led}\) minori di circa 1.80 V, mentre cresce rapidamente per valori maggiori. Il valore 1.8 V è appunto il “ginocchio” o “soglia” di potenziale del diodo, che indichiamo con \(V_s\).

Con un software di analisi dati si possono approssimare i dati con una funzione esponenziale dai cui parametri si può ricavare \(V_s\). Noi però abbiamo scelto di stimare tramite \(V_s\) un fit lineare, più semplice da presentare agli studenti, approssimando i dati per valori di \(V_{led}\) maggiori del “ginocchio” con l’andamento lineare:

\[I = m V_{led} + b\]
. La tensione di soglia \(V_s\) la si ottiene per I = 0 e quindi è data dalla relazione: \(V_s = \large{\frac{-b}{m}}\).
Per il diodo di colore giallo la regressione lineare ha fornito i valori: 

\[m = ( 67 \pm 6)\ mA/V \quad b=(-123 \pm 14)\ mA\]

La tensione di soglia \(V_s\) e il suo errore risultano quindi:

\[\quad V_s = -b/m \rightarrow V_s = (1.8 \pm 0.2)\ V\]

Si procede in modo analogo per gli altri LED.

LED 2:  Verde \(\lambda = (577 \pm 16) nm\)

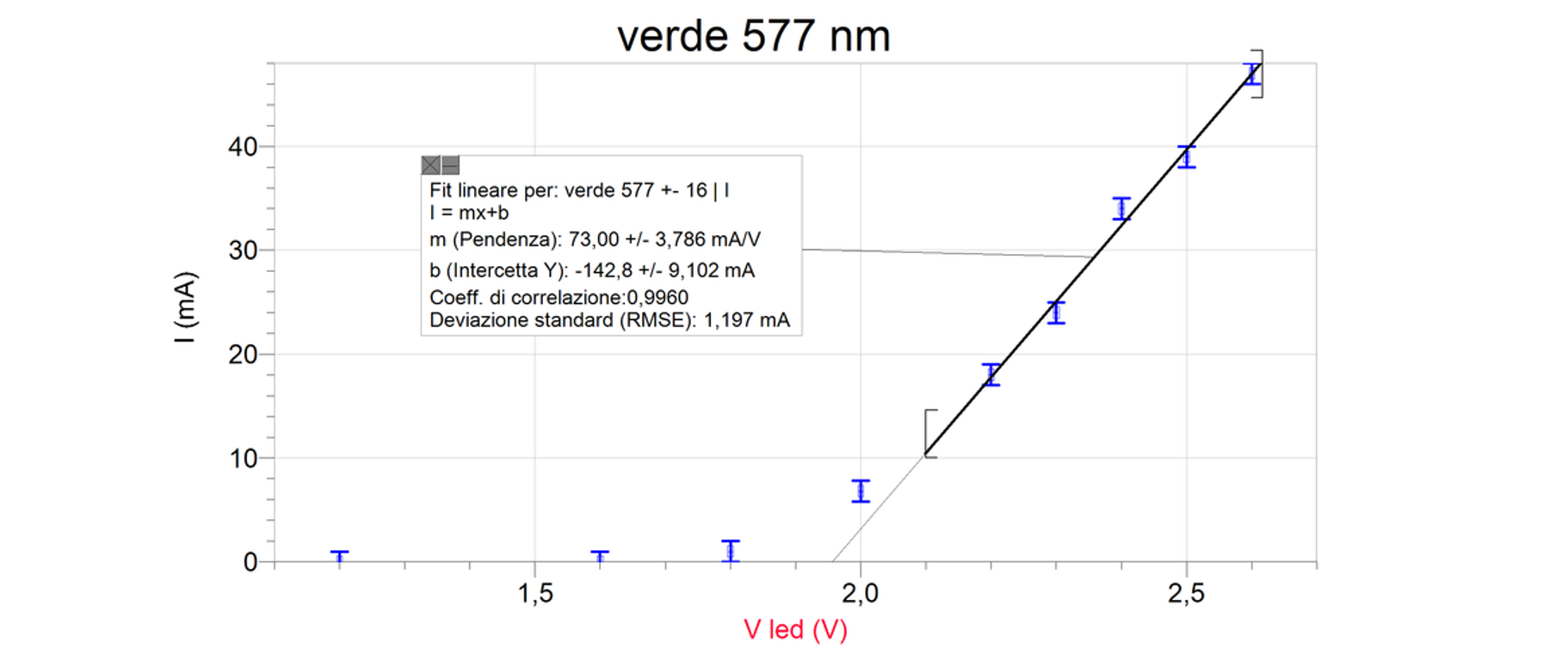
La retta di regressione lineare trovata è: 

\[m = (73 \pm 4) mA/V ; \quad b = (-143 \pm 9) mA\]

La tensione di soglia \(V_s\) e il suo errore sono:

\[I=0 ; \quad V_s = -b/m \rightarrow V_s = (2.0 \pm 0.2) V\]

LED 3:  Infrarosso \(\lambda = (963 \pm 55) nm\)

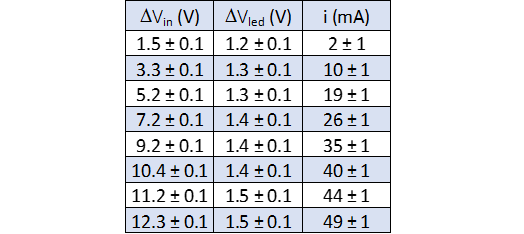
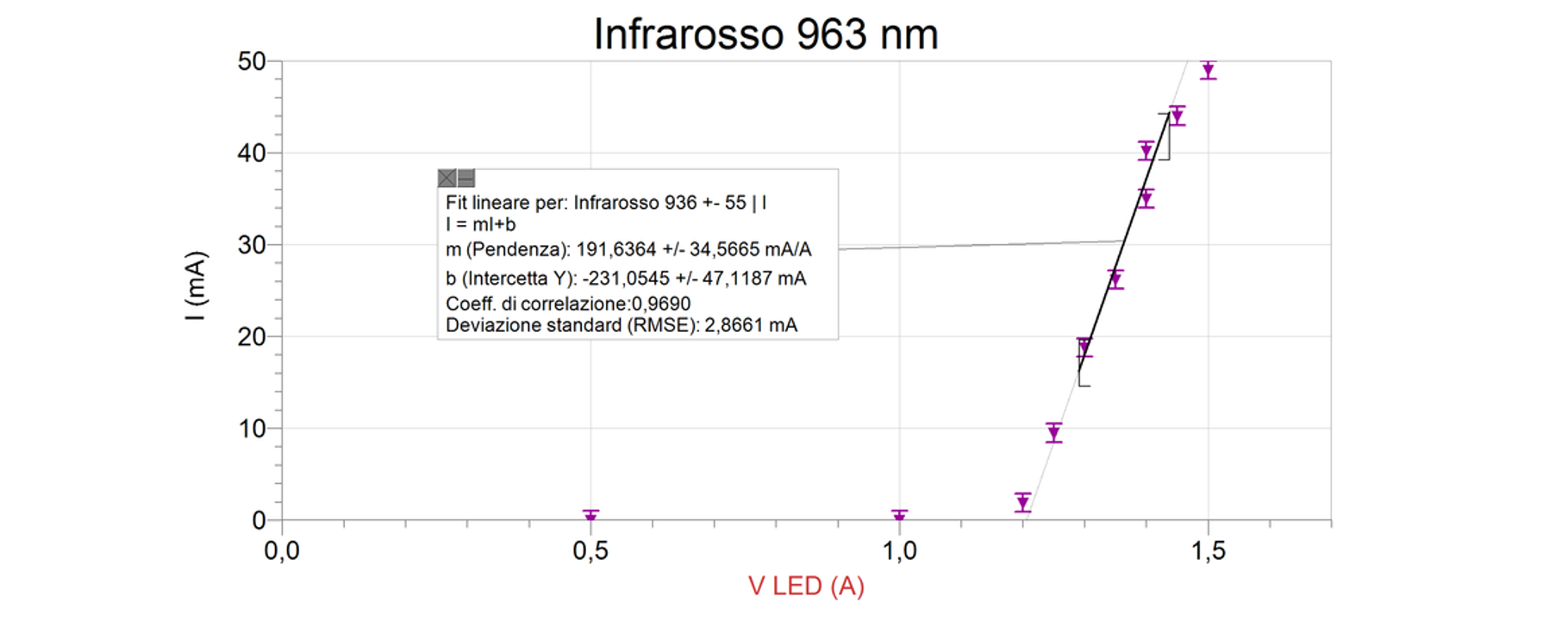
 La retta di regressione lineare trovata è:

\[m = (192 \pm 35) mA/V ; \quad b= (-231 \pm 47) mA\]

La tensione di soglia Vs e il suo errore:

\[I=0 ; \quad V_s = -b/m \rightarrow V_s = (1.2 \pm 0.4) V\]

LED 4:  Celeste-Violetto \(\lambda = (436 \pm 31) nm\)

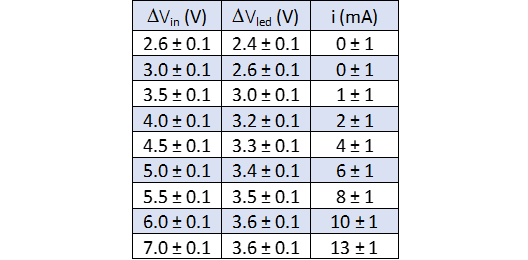
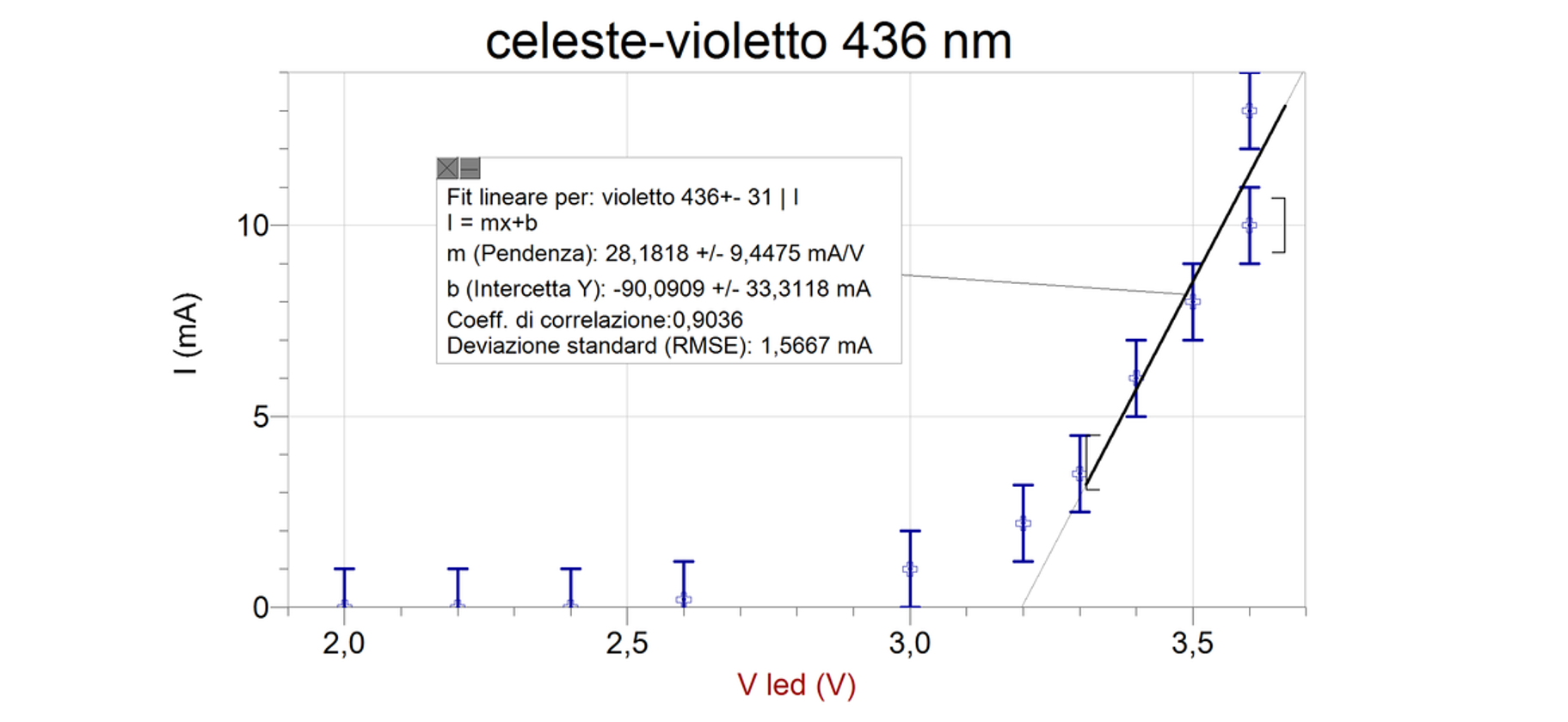
La retta di regressione lineare trovata è:

\[m= (28 \pm 9) mA/V ; \quad b = (-90 \pm 33)mA\]

La tensione di soglia Vs e il suo errore:

\[I=0; \quad V_s = -b/m \rightarrow V_s = (3.2 \pm 1.4) V\]

I risultati ottenuti sono riepilogati in tabella 5.

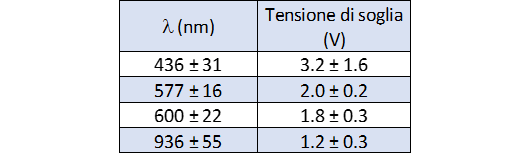
Parte II: Stima della Costante di Planck

Secondo l’ipotesi di Planck gli scambi di energia tra la radiazione e la materia avvengono in modo quantizzato. Einstein aggiunse che la radiazione stessa è composta da quanti (i fotoni) di energia proporzionale alla frequenza  ν, secondo la relazione:

\[E = hv \ \ \ \ \ \ \ \     [1]\]

dove h è la costante di Planck. 
In un LED alla soglia  l’energia acquistata da ogni portatore di carica nell’attraversare il diodo (pari alla differenza di potenziale ai capi del led moltiplicato per la carica elementare) si trasforma tutta in un fotone secondo la relazione [1]. Possiamo quindi attenderci una relazione di proporzionalità diretta tra la tensione di soglia e la frequenza dei fotoni emessi data dalla relazione: \(\nu = c/\lambda\):

\[e V_s = h \nu \quad  [2]\]

con \(e = 1.6 \cdot 10^{-19} C\).

In tabella 6 sono riportati i dati della frequenza e dell’energia alla soglia per i diodi studiati:

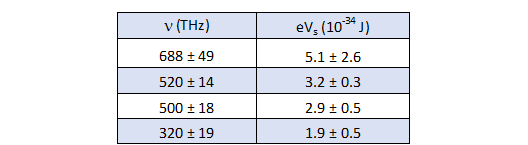
Eseguendo una regressione lineare sui dati di tabella 6, secondo la relazione [2] si ricava il seguente grafico:

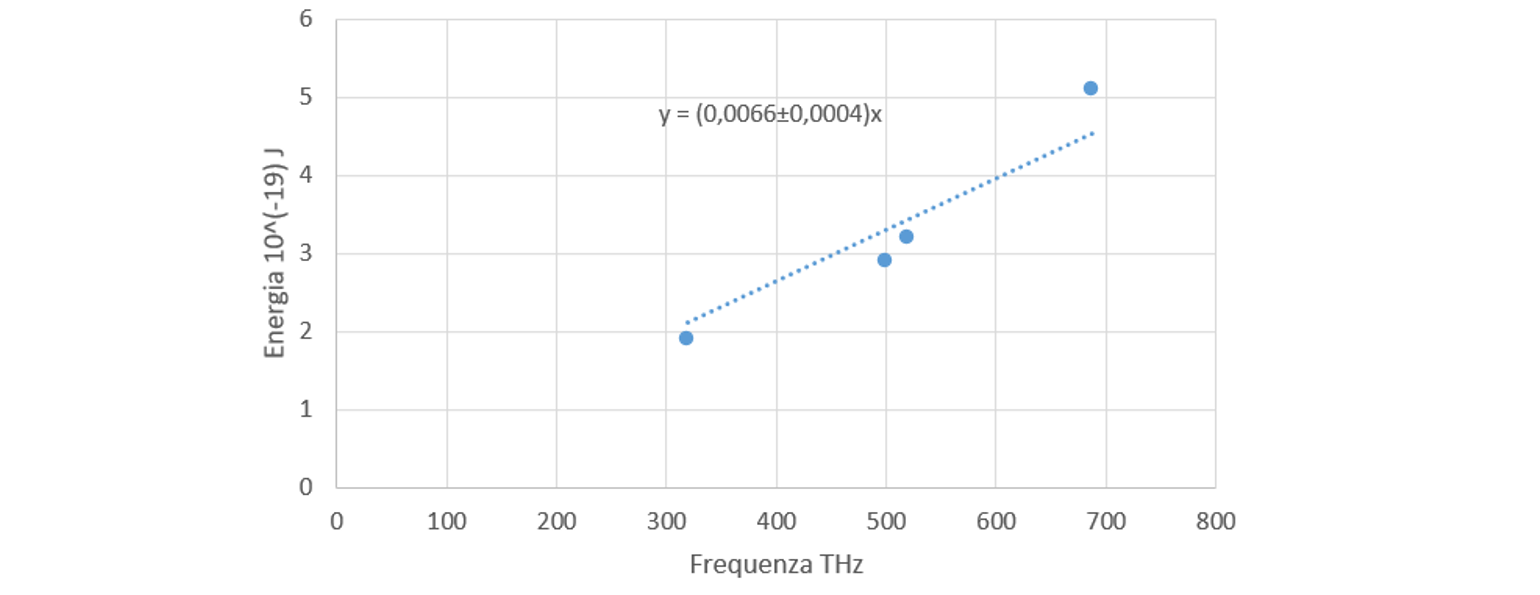
Il coefficiente angolare della retta rappresenta fisicamente la costante di Planck. Dai valori forniti dalla regressione lineare ottenuta fissando l’intercetta a zero, otteniamo il valore \(h = (6.6 \pm 0.4 ) 10^{-34} J \cdot s\), in accordo con il valore atteso di \(h = 6,626\  10^{-34}\ J \cdot s\).

Note e storia

L’esperimento è stato messo a punto nel corso di Preparazione di Esperienze Didattiche presso l’Università Federico II di Napoli

Autori

Asprino Filomena

Specifiche esperimento Materia Fisica Classi a cui è rivolto 5° anno Tipologia di laboratorio Strumentazione semplice Reperibilità del materiale Negozi specializzati, siti web Materiale specifico Led di diversi colori dall’infrarosso al violetto, generatore di tensione variabile, amperometro, voltmetro, resistenza elettrica, basetta per montare il circuito Durata esperimento in classe 1 h Capacità di bricolage/assemblaggio Sì Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Fisica moderna Fisica quantistica Effetto fotoelettrico Costante di Planck