Riassunto / Abstract

Un magnete sospeso grazie ad una molla viene messo in oscillazione all’interno di una bobina collegata ad un oscilloscopio. Nella bobina il moto oscillatorio induce una forza elettromotrice indotta. Il segnale acquisito con l’oscilloscopio permette di studiare il moto del magnete,  di verificare le previsioni teoriche, di stimare il campo magnetico prodotto dal magnete, di misurare la corrente indotta e di ipotizzare un’espressione analitica per interpolare il segnale indotto.

Scheda sintetica delle attività

• Sospendere molla e magnete tramite stativo;
• posizionare la bobina sotto il magnete, magari leggermente più in alto rispetto al banco;
• collegare le uscite della bobina ad un canale di acquisizione dell’oscilloscopio;
• attivare il trigger dell’oscilloscopio;
• tirare leggermente il magnete e lasciarlo oscillare;
• acquisire il segnale e fermare l’acquisizione;
• esportare il file sul PC oppure campionare da foto o da video usando un software di video-editing;
• eseguire l’analisi dei dati.

Risorse necessarie

• Stativo;
• molla;
• magnete cilindrico;
• cavi;
• oscilloscopio oppure Arduino;
• bilancia digitale (portata : 5000 g, sensibilità : 0,1 g);
• bobina;
• software di analisi dati;
• smartphone o macchina fotografica.

Prerequisiti necessari

• Saper manovrare un oscilloscopio e utilizzare un software per l’analisi dei dati;
• conoscenze di statistica;
• conoscenza del moto armonico e della legge di Faraday-Neumann-Lenz.

Obiettivi di apprendimento

• Studiare un oscillatore armonico smorzato valutando insieme aspetti meccanici ed elettromagnetici;
• giustificare,  sulla base delle leggi studiate,  un determinato esito sperimentale facendo ricorso a pratiche e procedure matematiche; 
• evidenziare bontà e limiti di un modello interpretativo anche in relazione agli strumenti tecnologici impiegati.

Dotazioni di sicurezza

Nessuna

Svolgimento

1. Montaggio dell’apparato sperimentale

L’apparato sperimentale è mostrato in figura 1.

La bobina presenta 12000 avvolgimenti, mentre la molla ha una costante elastica  elastica  \(K = (7,0 \pm 0,1) N/m\)    determinata sperimentalmente attraverso misure statiche. 
Il magnete cilindrico ha una massa \(m =  (53,0 \pm 0,1)g\).    
I terminali della bobina vengono collegati tramite due cavetti al canale 1 dell’ oscilloscopio. La bobina è stata appoggiata su un cilindretto di cartone per evitare che il magnete potesse urtare il tavolo. Il periodo di oscillazione atteso  é:

\[T = 2 \pi \sqrt{ \frac{m}{K}} = 0,55\ s\]

con un’incertezza sperimentale:

\[\sigma_T = \sqrt{\left(\frac{\sigma_K}{K}\right)^2 + \left(\frac{\sigma_m}{m}\right)^2} \cdot T = 0,01\ s\]

2. Settaggio dell’ oscilloscopio: 

Si imposta sull’asse dei tempi un intervallo di 500 ms/div., mentre per l’asse verticale della tensione si decide di regolare la scala durante le misure. Per la scala delle tensione viene impostato il valore di 2.00 mV/div.  

3.Misure di tensione e periodo 

Dal display dello strumento possiamo leggere una tensione di picco pari a \((2,8 \pm 0,1)V\). Misurando almeno quattro distanze picco -picco in orizzontale si ottengono i valori di tabella 1:

Il valore del periodo viene ricavato calcolando la media aritmetica dei valori misurati presenti nella tabella, mentre l’incertezza sulla media, ossia sul periodo, viene determinata attraverso la deviazione standard campionaria \(\sigma\) dei dati che risulta essere: \(\sigma = 0,065\ s\).

\[\bar{T} = \frac{1}{4} \sum_{i=1}^4 T_i = \left(0,68 \pm 0,03 \right)\ s\]

\[\sigma_{\bar{T}} = \frac{\sigma}{\sqrt{4}} = 0,03\ s\]

Il periodo sperimentale risulta maggiore e non compatibile entro gli errori con il periodo teorico. La discrepanza ravvisata potrebbe  dipendere dalla parte terminale della molla (dove si aggancia il magnete) che non contribuisce alla costante elastica della molla ma aggiunge “massa”. 
Un effetto di ritardo potrebbe essere dovuto anche all’azione del campo magnetico prodotto dalla corrente indotta nella bobina sul magnete stesso. Una stima del periodo di oscillazione in aria, senza la bobina, permetterebbe di verificare eventuali deviazioni sistematiche dal valore teorico. L’oscillatore armonico nella bobina dissipa più energia rispetto alla semplice oscillazione in aria poiché in questo caso parte dell’energia meccanica viene convertita in energia elettrica.

4. Stima del campo magnetico medio

Dalla lettura sull’asse dei tempi si  registra una durata  Δt = (200 ± 10) ms per la fase di estrazione  del magnete. Possiamo approssimare abbastanza bene l’area dell’impulso positivo con un trapezio di area (figura 3):

\[Area = \frac{100 + 40}{2}ms \cdot 2,60V=182 mV \cdot s\]

L’area rappresenta il flusso del campo magnetico concatenato con la bobina. Dividendo per la sezione della bobina e per il numero di spire si ottiene una stima del campo medio.
La bobina  ha sezione quadrata di lato medio pari a \(L = \left(4,5 \pm 0,1 \right) \cdot 10^{-2} m\) e perciò di area \(S = \left(20,3 \pm 0,9 \right) \cdot 10^{-4}\ m^2\). 
Il campo magnetico medio risulta essere:

\[B = \frac{Area}{N \cdot S} = 75\ G\]

Non è del tutto corretto calcolare il flusso di B concatenato con la spira attraverso la relazione:

\[\Phi \left(B\right) = NSB\]

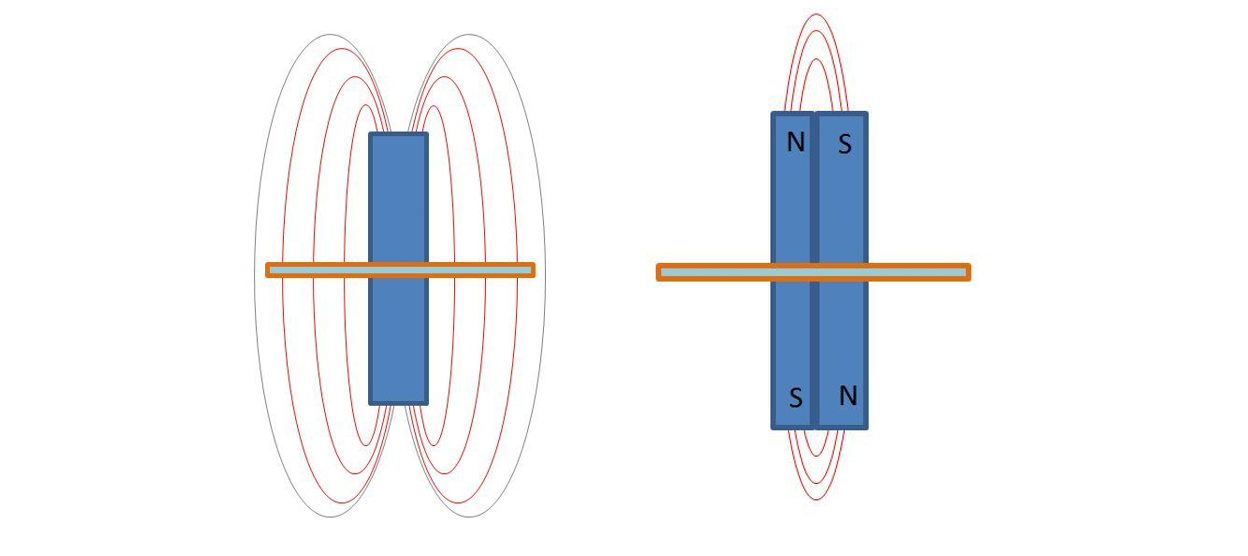
con S superficie della spira: infatti, come mostrato nella figura 4 a sinistra, le linee del campo che si chiudono senza incrociare la spira non contribuiscono al flusso, questo fa si che la corrente indotta sia inversamente proporzionale alla terza potenza del lato della spira.
Il fatto che le linee “esterne” alla spira non generano corrente si può verificare facendo oscillare due magneti accoppiati come in figura 4 immagine di destra: in questo secondo  caso le linee di campo sono chiuse e la fem indotta è bassissima.

5. Calcolo della corrente indotta nella bobina

Per determinare  la corrente indotta, la bobina va chiusa sul circuito d’ingresso dell’oscilloscopio o del tester, considerando sia la resistenza della bobina, che dovrebbe esser riportata sulla bobina stessa, che la resistenza introdotta da questi strumenti. Qualora la resistenza di bobina non fosse riportata, la si calcola con  la seconda legge di Ohm. La lunghezza del filo è pari a ad N perimetri della sezione di spira,  Dividendo la tensione indotta per il valore della resistenza complessiva si perviene alla corrente I(t) indotta.

6. Interpolazione statistica del segnale indotto

 Campionando il segnale di tensione  positivo attraverso lo schermo si ricava una tabella e un grafico su cui è possibile eseguire un fit.  Si può assumere un errore di  5 ms per i tempi e di 10 mV  per le tensioni.

Una gaussiana fitta abbastanza bene un semi-periodo del segnale. Si può integrare la funzione così campionata e confrontare il risultato con la stima iniziale. 

L’integrale definito della f.e.m. indotto, dopo opportuno campionamento è stato calcolato mediante software LOGGER PRO e il valore di area restituito risulta:

\[Area = 292 mV \cdot s\]

Da notare che si tratta comunque di un valore approssimato, poiché il software utilizza la poligonale dei dati campionati. Usando una calcolatrice è possibile calcolare l’integrale della funzione gaussiana utilizzata nel fit:

\[Ae^{- \frac{\left(t-B\right)^2}{C^2}}\]
con \(A = 2,837\), \(B =  – 0,113\) e \(C = 0,058\), valori ottenuti dal fit (figura 5):

\[\int_{-0,3}^{0}2,837 \cdot e^{-\frac{\left(t+0,113\right)^2}{0,058^2}}dt =291 mV \cdot s\]

Valori decisamente migliori della stima iniziale effettuata con l’approssimazione del trapezio. Va anche detto che l’area ottenuta non è unitaria poiché la funzione integranda non è la gaussiana normalizzata.

La stima di qualità del fit eseguito con il software LOGGER PRO, di proprietà della VERNIER, è la RMSE, riportata insieme alla funzione interpolante. La RMSE non ha valore assoluto. Più la RMSE è piccola migliore sarà l’interpolazione, tuttavia non raggiunge l’affidabilità del \(\chi ^2\). La RMSE è la varianza della distribuzione dei residui rispetto al valore d’interpolazione, ossia la  formula di Fisher:

\[RMSE = \sqrt{\frac{\sum \left( f(x_i)-y_i \right)^2}{n-R}}\]

dove n  è il numero di misure ed R il numero dei parametri. 

Molte delle misure sinora effettuate  si possono ottenere anche senza un oscilloscopio, ma con il microcontrollore  Arduino,  riportando nell’ingresso analogico \(A_0\) la tensione indotta nella bobina.

7. Studio dell’attenuazione

Osservando sull’oscilloscopio il segnale indotto, si nota una leggera attenuazione (figura 7) riconducibile al moto viscoso in aria e, in forma molto minore, all’effetto di induzione elettromagnetica che si manifesta come una forza sul magnete che si oppone sempre al suo moto. La bobina respinge il magnete nella fase di avvicinamento e lo attrae in quella di allontanamento. Da uno studio sui soli picchi del segnale indotto, si ha la seguente attenuazione esponenziale:

 L’attenuazione è ben descritta da un’esponenziale decrescente esprimibile in volt:

\[V(t) = 0,3 \cdot e^{-0,5t} + 1,7\]

Lo smorzamento osservato è riconducibile in misura non trascurabile all’interazione  tra magnete e bobina spiegabile in termini di energia necessaria per indurre una corrente nella bobina, parimenti dissipata per effetto Joule. Dal momento che: 

\[I_{indotta} = \frac{fem(t)}{R}\]
La potenza dissipata è:        

\[P = \frac{(fem)^2}{R}\]

La fem è proporzionale alla velocità del magnete, dal momento che il flusso cambia in ragione del cambiamento  del campo magnetico che dipende da come la distanza magnete-bobina varia nel tempo, quindi:

\[P = \alpha \frac{v^2}{R}\]

La  potenza dissipata è quindi quella di una forza proporzionale alla velocità, analoga all’attrito viscoso per flusso laminare.
La dipendenza \(1/R\) merita un approfondimento. Se la bobina viene chiusa su un rivelatore di corrente (amperometro a bassa resistenza interna) l’effetto di smorzamento è molto più evidente che se viene chiusa su un voltmetro ad alta resistenza. Questo spiegherebbe la differente attenuazione osservata usando l’oscilloscopio ed ARDUINO come mostrato in figura 8.

Dallo studio dell’attenuazione otteniamo:

In questo caso l’attenuazione è descritta dall’esponenziale (figura 9):

\[V(t) = 1,786 \cdot e^{-0,159 t} + 0,231\]

A parità di valore iniziale(circa 2,0 V) e prescindendo dai differenti valori di OFFSET, l’attenuazione ottenuta con l’oscilloscopio è più marcata. 

8.Studio del moto del magnete

Quanto ad una descrizione del moto del magnete, non trattandosi di un solenoide o di una bobina a sezione circolare, è piuttosto arduo, se non impossibile,  schematizzare il  magnete come un semplice conduttore percorso da corrente e sottoposto a forze magnetiche di campi noti. Sicché la scrittura di un’equazione differenziale che descriva il moto periodico smorzato (non armonico) non è pensabile, tanto più in una classe di liceo.  Si rimanda all’approfondimento allegato. 

Note e storia

Vedasi gli allegati “Dipolo magnetico e induzione elettromagnetica”  e “interazione bobina – magnete con masse magnetiche” per un approfondimento sullo studio del moto del magnete

Bibliografia

• J.R. Taylor, Introduzione all’analisi degli errori – Lo studio delle incertezze nelle misure fisiche, ZANICHELLI, Bologna 1990;
• Mazzi, P. Ronchese, P. Zotto, Fisica in Laboratorio – Esperienze per i corsi di Fisica in ingegneria, Società Editrice Esculapio, Grisignano(VI) 2013;
• L. Gregorio, Il dipolo magnetico ed il fenomeno di induzione, Liceo Scientifico “Galilei” di Napoli, 2008. Disponibile sul sito www.luigigregorio.it.

Autori

Di Iorio Giacomo

Schede / Allegati

• Dipolo magnetico e induzione elettromagnetica
• interazione bobina – magnete con masse magnetiche
• programmino per ARDUINO

Relazioni

• Arduino, oscillatore armonico e f.e.m.i.

Specifiche esperimento Materia Fisica Classi a cui è rivolto 2° biennio Tipologia di laboratorio Attrezzato Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Oscilloscopio, bilancia, magnete, molla, bobina Durata esperimento in classe 4 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Elettromagnetismo Induzione elettromagnetica Corrente indotta Moto armonico smorzato