Riassunto / Abstract

Si propone di verificare o ricavare le leggi di Ohm utilizzando un matita per tracciare circuiti, collegamenti e resistenze estese. 
In maniera semplificata può essere utilizzato per discutere di misure, grafici ed errori in classi I (il programma di terza media prevede le leggi di Ohm). Può essere presentato alle classi IV o V per quel che riguarda i fenomeni elettrici. Osservare l’effetto della temperatura può essere lo spunto per discutere di conduttori, isolanti, semiconduttori e materiali moderni.

Scheda sintetica delle attività

Si misura la resistenza di strisce disegnate a matita su un foglio di carta, verificando che:

• a parità di larghezza, la resistenza di una striscia di grafite è direttamente proporzionale alla sua lunghezza;
• parità di lunghezza la resistenza di una striscia di grafite è inversamente proporzionale alla sua larghezza.

L’esperienza è usata per discutere di:

• incertezze ed errori di misura;
• media, errore della media;
• regressione lineare.

Nell’esperienza si fa uso di fogli elettronici per il trattamento e l’analisi dei dati sperimentali.

Risorse necessarie

• Carta a quadretti o millimetrata;
• matita, attenzione non tutte le mine rispondo allo stesso modo: le mine morbide e di buona qualità contengono più grafite e sono da preferirsi;
• forbici;
• multimetro (analogico o digitale).
• centimetro o calibro;
• eventualmente un foglio elettronico (es. Excel o Calc) per l’analisi dei dati sperimentali.

Prerequisiti necessari

• Nozioni di base su correnti, tensione e resistenza;
• saper utilizzare un multimetro;
• conoscere la II legge di Ohm \(R = \rho \large{\frac{L}{S}}\);
• media e deviazione standard.

Obiettivi di apprendimento

• Trattamento dei dati: media e deviazione standard;
• errore sulla media;
• grafici xy ed errori di misura;
• calcolo della regressione lineare.

Dotazioni di sicurezza

Nessuna

Svolgimento

Introduzione

La II legge di Ohm stabilisce che la resistenza di un conduttore è direttamente proporzionale alla sua lunghezza (L) e inversamente proporzionale alla sezione (S):

\[R = \rho \frac{L}{S}\ \ \ \ \ \ [1]\]

dove ρ [Ω m] è la resistenza per unità di lunghezza del materiale.

La mina di una matita è fatta principalmente di grafite, cioè Carbonio, che a temperatura ambiente, si comporta da conduttore. Si vuole verificare la [1] misurando la resistenza di strisce disegnate a matita su un foglio di carta. Conviene lavorare in gruppi di due tre persone.

Nota: non è necessaria una strumentazione particolarmente precisa, sarà anzi utile discutere l’origine e l’entità delle incertezze di misura, tra queste:

• uniformità e riproducibilità dello spessore degli strati di grafite;
• accuratezza nella forma delle strisce;
• precisione nella posizione dei contatti;
• effetto della pressione sui contatti;
• diversa composizione della mina (le mine più dure contengono un’elevata frazione di argille e risultano del tutto isolanti).

Gruppi diversi otterranno probabilmente valori diversi pur riproducendo l’andamento corretto delle curve.

Non è semplice ottenere un valore stabile e riproducibile della misura di resistenza. Andranno fatte alcune prove per capire la migliore strategia, ad esemio usare dei coccodrilli o pinzette è sicuramente meglio dei puntali.

Osservando i primi risultati stimolare la riflessione su come considerare le cifre significative della misura con : i multimetri digitali forniscono risultati con parecchie cifre decimali, tuttavia un’approssimazione a una due cifre decimali è sicuramente più ragionevole.

Stante l’ampia dispersione dei risultati è ragionevole utilizzare la media \(\bar{x}\) di 4-5 misure per migliorare la precisione, data da:

\[\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i\]

L’errore sulla media è calcolato (teorema del limite centrale), in accordo con le indicazioni del Bureau International des Poids et Mesures (BIPM) come il rapporto tra la deviazione standard e la radice quadrata del numero di misure:

\[\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{N}}\]
dove

\[\sigma =\sqrt{\frac{1}{N-1}\sum_{i=1}^N\left(x_i – \bar{x} \right)^2}\]

E’ utile iniziare con una discussione sull’errore di misura e l’errore sulla media.

Dipendenza dalla lunghezza (L)

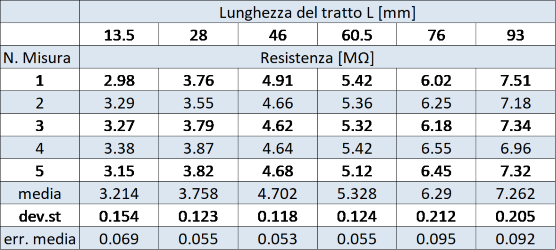
Si disegna un tratto di larghezza pari a 1 quadretto e lungo una decina di cm. Si misura quindi la resistenza in funzione della lunghezza; i valori ottenuti sono riportati in tabella 1. Il file Excel (vedi Scheda 38-xls ) può essere usato come guida.
Nota: non sono riportati gli errori di lettura sulla singola misura dal momento che sono trascurabili rispetto all’incertezza che si riscontra confrontando misure successive.

.

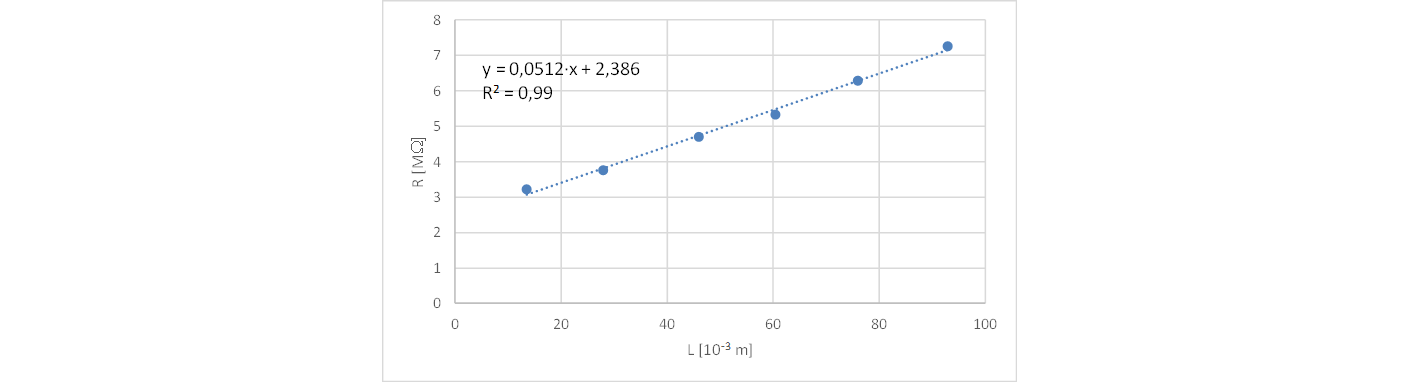
Figura 2 riporta il grafico dei valori medi della resistenza in funzione della lunghezza; è evidente l’andamento lineare, che può essere evidenziato meglio utilizzando una retta di regressione. Anche qui un foglio elettronico semplifica il trattamento: stimolare gli studenti a trovare le funzioni corrette nel foglio elettronico.
 Il coefficiente angolare della retta di regressione \(m= 0,0512\ M\Omega/m\) è pari al  rapporto \(m = \large{\frac{\rho}{S}}\). 

Discutere qui quanto le possibili sorgenti di incertezza viste sopra abbiano effettiva influenza sull’andamento osservato.

I risultati sperimentali mostrano una chiara differenza con l’andamento atteso in base alla [1], in particolare la retta di regressione ottenuta dai dati sperimentali, \(R=m \cdot L + c\) , non passa per l’origine.

Possiamo ipotizzare che la resistenza ai contatti sia responsabile di questo comportamento. 
Come si può verificare questa ipotesi?
Come si può ridurre la resistenza ai contatti? (aumentare la superficie, utilizzare contatti differenti etc…).

Dipendenza dalla sezione (D)

Per questa parte conviene preparare una striscia molto larga e, senza staccare i contatti, misurare la resistenza tagliando via progressivamente una striscia dai bordi. Altre strategie sono ugualmente possibili ed efficienti. In effetti stiamo assumendo che lo spessore della striscia sia costante, quindi la variazione di sezione è determinata solo dalla larghezza D. Come nel caso precedente si effettua un certo numero di misure per ogni sezione; i valori ottenuti sono riportati in tabella 2. 

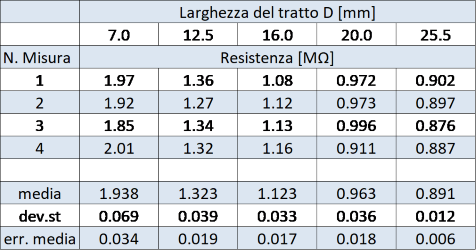
Riportando su un grafico R in funzione di D, si vede chiaramente come questo non abbia un andamento lineare (figura 3, sinistra).

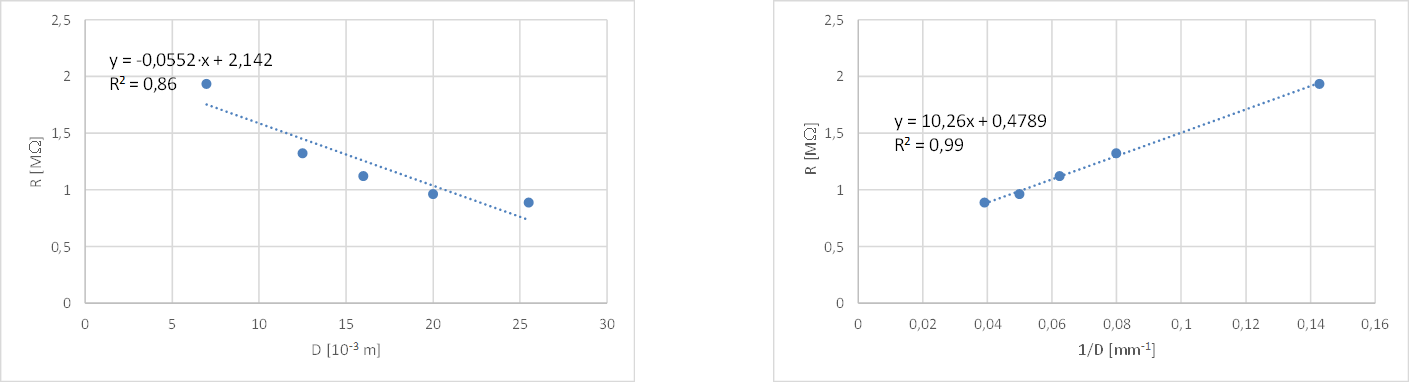
Tuttavia riportando su un grafico R in funzione di 1/D, l’andamento risulta essere lineare (figura 3, destra).

Infatti indicando con t lo spessore del tratto, assunto costante, e con \(z = \large{\frac{1}{D}}\) abbiamo:

\[R = \rho \cdot \frac{L}{S} =  \rho \cdot \frac{L}{t \cdot D}= \left(\rho \frac{L}{t} \right) \cdot z\]

L’andamento previsto è quindi lineare con \(z = \large{\frac{1}{D}}\); il coefficiente angolare della retta è proporzionale alla resistività \(\rho\) e alla geometria della striscia, in particolare al rapporto \(\large{\frac{L}{t}}\). 
Anche in questo caso la retta di regressione non passa per l’origine a causa del contributo dei contatti.

Effetto della temperatura

Scaldando il film (ad esempio poggiando il foglio su una lampadina o utilizzando un asciugacapelli) la resistenza decresce sensibilmente. E’ questo un comportamento diverso da quello che succede in un metallo (ad esempio misurando la resistenza di un avvolgimento di rame). 
Si può innestare una discussione sul differente comportamento elettrico di conduttori e  semiconduttori come la grafite. 

Note e storia

Si potrebbe proporre in modo relativamente semplice un esperimento che mostri l’analogo idraulico della legge di Ohm usando cannucce e bottiglie e acqua. é decisamente istruttivo per gli alunni.

Bibliografia

• La legge di Ohm (Wikipedia.it & wikipedia.en)
• Il multimetro 

Autori

Meneghini Carlo

Schede / Allegati

• Analisi dei dati

Specifiche esperimento Materia Fisica Classi a cui è rivolto 2° biennio Tipologia di laboratorio Strumentazione semplice Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Multimetro, centimetro o calibro, forbici, carta millimetrata Durata esperimento in classe 1,5 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Elettromagnetismo Corrente elettrica Legge di Ohm Resistenza elettrica