Riassunto / Abstract
Si misura la costante di tempo per la scarica di un condensatore (circuito RC) usando una bilancia da cucina, due piastre e resistenze di carta.
Scheda sintetica delle attività
Si ricava la legge che descrive l’andamento della scarica di un condensatore, misurando diverse costanti di tempo di scarica in funzione dell’inserimento nel circuito elettrico di differenti resistenze in serie al condensatore.
Risorse necessarie
- Bilancia da cucina (1g);
- racchetta anti-zanzare;
- due piastre di alluminio (circa: 25 x 30 x 3 mm3 , devono essere abbastanza spesse da non flettere);
- fili per contatti elettrici;
- supporti in legno (devono consentire di mantenere una distanza di circa 1 mm tra le lastre);
- cellulare o videocamera;
- foglio di carta;
- centimetro o squadretta per misure lineari;
- foglio elettronico.
Prerequisiti necessari
- Saper montare un circuito elettrico;
- concetti di posizione, velocità, accelerazione, massa, forza, energia, campo elettrico e gravitazionale;
- utilizzo di strumenti matematici elementari (e.g. derivate, prodotto scalare e vettoriale, integrali);
- capacità di usare un software di analisi dati (e.g. foglio Excel);
- saper costruire e leggere un grafico.
Obiettivi di apprendimento
- Saper ricavare la legge che descrive la scarica di un condensatore;
- approfondire la scarica di un condensatore in un circuito RC in funzione della variazione della resistenza del circuito;
- indagare la dipendenza tra la costante di tempo relativa alla scarica del condensatore e la forza di Coulomb tra le due piastre.
Dotazioni di sicurezza
Aspettare sempre che le piastre si scarichino completamente (può volerci qualche minuto) per evitare di prendere una piccola scossa (in ogni caso non pericolosa) ed eventualmente usare guanti in silicone per maneggiare l’attrezzatura.
Svolgimento
Allestimento
Il condensatore viene realizzato usando due piastre di alluminio poste l’una sopra l’altra ad una certa distanza e caricate sfruttando la d.d.p. generata da una racchetta anti-zanzare.
- Posizionare una lastra sulla bilancia e tararla su 0 grammi.
- Poggiare la seconda lastra sui supporti e posizionarla sopra la prima, assicurandosi che le due lastre non si tocchino.
- Realizzare un circuito elettrico usando una racchetta anti-zanzare (generatore del circuito) e due fili per contatti elettrici: collegare le due estremità dei due fili alla racchetta e le altre due alle due piastre.
- Dopo la prima misura inserire un foglio di carta nel circuito (che agisce come un resistore): aumentando la distanza tra i morsetti attaccati sul foglio si aumenta la resistenza associata al foglio di carta.
Il setup sperimentale è mostrato in figura 1.

Introduzione
Considerando che il sistema costituito dalle due piastre (condensatore) e dalla racchetta anti-zanzare (generatore) è un sistema isolato, l’energia totale si conserva. Le forza agenti sono la forza peso
\[F_p = m \cdot g = – F_e\]
La forza attrattiva tra le armature di un condensatore può essere scritta come
\[F_e = \frac{1}{2}\frac{Q^2}{\epsilon_0 \cdot S}\]
dove \(Q\) è la carica accumulata tra le armature, \(\epsilon_0\) la costante dielettrica del mezzo tra le armature (in questo caso aria) e \(S\) la superficie del condensatore.
Assumendo che il generatore (ovvero la racchetta anti-zanzare) fornisca sempre la stessa d.d.p. al condensatore, verrà accumulata sempre la stessa carica sulle piastre. Una volta premuto l’interruttore della racchetta, la bilancia misura una massa che risulta proporzionale alla forza elettrostatica con cui la lastra superiore attrae quella inferiore e di conseguenza al quadrato della carica immagazzinata (poiché restano costanti \(\epsilon_0\) e la superficie del condensatore):
\[F_e \propto m \propto Q^2\]
Partendo da queste premesse teoriche, l’esperimento qui descritto si propone di studiare l’andamento della scarica di un condensatore in un circuito RC in funzione delle variazioni della resistenza.
Misure e Analisi Dati
Per poter graficare la carica in funzione del tempo e ricavare la costante di tempo della scarica del condensatore è necessario calcolare la superficie del condensatore, misurando con un semplice righello o una squadra i lati delle piastre di alluminio.
I dati qui riportati fanno riferimento ad un condensatore con una superficie \(S \simeq \left( 22 \cdot 22,7 \right)\ cm^2 \simeq 500\ cm^2)\) ovvero circa \(0,5\ m^2\); la costante dielettrica è quella del vuoto è: \(\epsilon_0 = 8,85 \cdot 10{-12}\ F/m\).
La forza attrattiva tra le armature si ricava moltiplicando la massa misurata sulla bilancia per l’accelerazione gravitazionale \(g = 9,81\ m/s^2\).
Infine, per ottenere la carica, occorre invertire la formula che esprime la forza elettrostatica per un condensatore piano:
\[Q^2 = 2 \epsilon_0 S \cdot F_e\]
Per la misura si può registrare un video e leggere successivamente con un programma di video-editing (ad esempio Avidemux) la massa misurata dalla bilancia in funzione del tempo.
Se le piastre sono troppo vicine è possibile ci siano delle scariche (rottura dielettrica), in questo caso si può aumentare la distanza inserendo spessori di carta.
Nella tabella in allegato vengono riportati i valori di \(Q^2\) a partire dal tempo \(t=0\) in cui viene premuto l’interruttore della racchetta anti-zanzare (ovvero viene acceso il generatore del circuito), considerando intervalli di \(\Delta t=1 s\).
Come mostrato nei video allegati è stato utilizzato un foglio di carta A4 come resistore. I diversi valori \(R_i\) sono stati ottenuti variando la distanza tra i morsetti attaccati al foglio di carta. Il valore \(R_0\) si riferisce al circuito “generatore + condensatore”, senza l’aggiunta del resistore (ovvero del foglio A4). Da \(R_1\) a \(R_3\) si incrementa il valore della resistenza variando la distanza tra i contatti.
Di seguito vengono riportati i corrispondenti grafici fittati per mezzo della funzione esponenziale
\[y = A_1 e^{-x/t_1} + y_0\]
in cui è stato imposto \(y_0 = 0\).
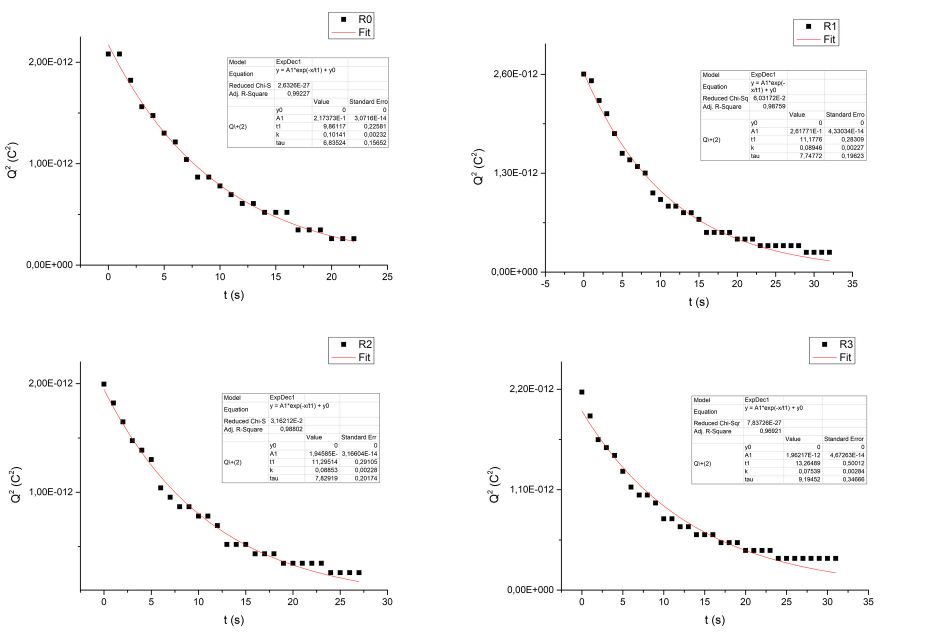
Il fit restituisce il valore del parametro \(t_1\) che, nel caso dell’esperimento qui considerato, corrisponde alla costante di tempo di scarica del condensatore \(\tau\).
Figura 3 mostra il grafico della costante di tempo \(\tau\) in funzione della resistenza R; notare come essa aumenti in funzione della distanza degli elettrodi indicando un aumento delle resistenza del foglio di carta all’aumentare della distanza tra gli elettrodi. Diversi fattori possono influire sulla resistenza del foglio, tra questi disomogeneità, la geometria non lineare. Risultati diversi ottenuti da diversi gruppi e la discussione con gli studenti fornisce un valido strumento per approfondire concetti quali resistenza, resistività, corrente elettrica, etc… Ad esempio quale può essere la forma ideale per la resistenza del foglio di carta? cosa succede se si mettono due strisce di carta una sull’altra (resistenze in parallelo).
.

Da notare che la resistenza del foglio di carta è di diversi \(M\Omega\), difficile da reperire in un laboratorio.
Discussione
Si consideri il circuito RC mostrato nella seguente figura:

CARICA DEL CONDENSATORE
Nel momento in cui l’interruttore S viene chiuso, una corrente scorre per breve tempo nel circuito e, contemporaneamente, le armature del condensatore si caricano. La massima carica \(Q_0\) che può accumularsi dipende dalla capacità \(C\) del condensatore e dalla tensione \(V_0\) fornita dal generatore ed è pari a:
\[Q_0 = C V_0\]
Se l’interruttore viene chiuso al tempo \(t=0\), il circuito è percorso da una corrente la cui intensità iniziale è data dalla legge di Ohm:
\[I_0 = \frac{V_0}{R}\]
Ad un certo istante successivo il condensatore avrà accumulato la massima carica possibile e di conseguenza la corrente che percorre il circuito si ridurrà a zero.
Durante la fase di carica, la d.d.p. tra le armature del condensatore e l’intensità di corrente variano nel tempo, secondo le seguenti leggi esponenziali:
\[V_C = V_0 \left(1-e^{-t/RC}\right) \hspace{2 cm} I = I_0 e^{-t/RC}\]
Analogamente, l’andamento della carica che si accumula sulle armature del condensatore sarà descritto da:
\[Q = Q_0\left(1-e^{-t/RC}\right)\]
La velocità di carica e scarica del condensatore può essere espressa attraverso la costante di tempo \(\tau =RC\). Per capirne il significato basta considerare che al tempo \(t=\tau=RC\) la d.d.p. tra le armature del condensatore è pari a \(V \simeq 0,63 V_0\) ovvero il condensatore è carico al 63% (al contrario l’intensità di corrente si è ridotta del 37%). Al tempo \(t = 2 \tau\) la carica del condensatore è più dell’86% del suo valore massimo, e così via…
SCARICA DEL CONDENSATORE
Si supponga ora di aprire l’interruttore S al tempo t=0, dopo aver lasciato caricare il condensatore. Quando un condensatore completamente carico viene scaricato attraverso una resistenza, la d.d.p. tra le armature decade esponenzialmente
\[V_C = V_0 e^{-t/RC} = V_0 e^{-t/\tau}\]
così come l’intensità di corrente e la carica:
\[I = I_0 e^{-t/\tau} \hspace{2 cm} Q = Q_0 e^{-t/\tau}\]
Note
I dati riportati fanno riferimento al quadrato della carica, di conseguenza la formula che esprime l’andamento dei dati sperimentali è
\[Q^2 = Q_0^2 e^{-2t/\tau}\]
che è sempre di tipo esponenziale.
OSSERVAZIONE: Come visto nella discussione, la costante di tempo per la scarica del condensatore è \(\tau = RC\) e di conseguenza risulta direttamente proporzionale al valore della resistenza \(R\). Ci si aspetta quindi un andamento lineare di \(\tau\) in funzione di \(R\), tuttavia la resistenza del foglio potrebbe non essere lineare in funzione della distanza tra gli elettrodi.
SVILUPPI: Per ottenere dei risultati più precisi ed attendibili sarebbe interessante utilizzare diverse resistenze note disposte in serie e, come verifica, dal valore di \(\tau\) si potrebbe calcolare \(R\), tenendo a mente che la capacità di un condensatore piano può essere scritta come
\[C = \epsilon_0 \cdot \frac{S}{d}\]
con \(d\) distanza tra le armature.
Autori
Meneghini Carlo
Carlini Laura
Schede / Allegati
Specifiche esperimentoMateria Fisica Classi a cui è rivolto 2° biennio Tipologia di laboratorio Strumentazione semplice Reperibilità del materiale Uso quotidiano, negozi specializzati, siti web Materiale specifico Piastre metalliche, racchetta anti-zanzare, bilancia Durata esperimento in classe 2 h Capacità di bricolage/assemblaggio Sì Necessità lavorazioni meccaniche/elettroniche Sì Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Elettromagnetismo Elettrostatica Forza di Coulomb Costante di tempo |