Riassunto / Abstract

Lo scopo dell’attività è lo studio del moto libero di una palla lanciata con velocità iniziale non nulla. L’attività è svolta usando il software Tracker (1) che permette di visualizzare e trattare la traiettoria del corpo usando una analisi dei video registrati. Tracker costituisce un’ottima risorsa per effettuare esperimenti anche fuori del laboratorio e/o in assenza di un laboratorio attrezzato.

Scheda sintetica delle attività

A scuola si effettua il filmato del lancio di una palla con un cellulare, dopo aver predisposto  la scena con gli opportuni accorgimenti.
A casa, come compito, gli studenti lavorano singolarmente per analizzare il filmato con Tracker:

1. tracciano la palla in volo;
2. analizzano i dati così raccolti;
3. costruiscono con Tracker i grafici x=x(t), y=y(t) e y=f(x);
4. interpretano i grafici;

A scuola viene effettuato il confronto tra i risultati ottenuti e la discussione.

Risorse necessarie

• Palla;
• asta graduata;
• cellulare;
• software Tracker;
• computer;

Prerequisiti necessari

• Conoscere le leggi del moto parabolico;
• saper utilizzare Tracker;
• saper leggere un grafico.

Obiettivi di apprendimento

• Verificare che un grave lanciato con una velocità iniziale orizzontale o obliqua descrive una traiettoria parabolica;
• verificare che il moto di cui è animato il grave è la composizione di due moti: uno rettilineo uniforme lungo l’asse delle ascisse e l’altro rettilineo uniformemente accelerato lungo l’asse delle ordinate;
• confrontare il valore sperimentale dell’accelerazione di gravità con quello teorico;
• incrementare la capacità di utilizzo del software Tracker.

Dotazioni di sicurezza

Nessuna

Svolgimento

Lo svolgimento è stato diviso in 4 fasi. La prima e l’ultima sono state svolte a scuola, dal gruppo classe nel suo insieme. Le altre due sono state svolte a casa dagli studenti. Si è scelto di farli lavorare singolarmente per permettere loro di imparare a utilizzare Tracker (il lavoro è stato preceduto da una veloce presentazione del software da parte della docente).

PRIMA FASE

1. Per permettere a Tracker di calibrare le distanze, bisogna prima di tutto scegliere un oggetto di riferimento disposto orizzontalmente o verticalmente e misurarne la lunghezza (a questo scopo abbiamo fissato alla parete che fa da sfondo nel filmato un’asta graduata lunga 1 m).
2. Si lancia una palla, che deve avere un colore facilmente distinguibile rispetto a quello dello sfondo.
3. Con un cellulare (alla velocità di 30 fps) si filma il moto della palla.
   Questa è una delle fasi più delicate, dalla quale dipende la buona riuscita dell’esperimento.
   Si consiglia di effettuare le riprese con il cellulare (o la videocamera) ben fisso su un cavalletto per evitare di sovrapporre al moto della palla quello del cellulare stesso.
   Prestare attenzione a lanciare la palla parallelamente al muro e a porre il cellulare nella stessa posizione per evitare effetti di deformazione della traiettoria.
   

SECONDA FASE

1. Si avvia Tracker e si importa il filmato realizzato.
2. Si selezionano i fotogrammi da analizzare (il filmato sicuramente parte prima del lancio della palla e termina quando questa ha concluso il suo volo per cui bisogna eliminare i fotogrammi che devono essere analizzati). La fase più delicata è quella della scelta del fotogramma iniziale (assicurarsi che la palla non sia più a contatto con le mani di chi la lancia).
3. Si calibra la scala utilizzando l’asta graduata precedentemente fissata al muro.
4. Si sceglie il sistema di riferimento. 
   E’ difficile, se non quasi impossibile, posizionare l’origine nel punto di inizio della caduta. L’importante è porre l’asse x perfettamente parallelo al pavimento.

TERZA FASE

1. Si sceglie dal menù principale la voce Tracce  e dal menù a tendina la voce Nuovo… “Punto di massa”.
2. Si associa al Punto di massa  la palla, selezionandola nel primo fotogramma del filmato.
3. La si traccia durante il movimento (la si segue, evidenziando la posizione che occupa, fotogramma per fotogramma). 
   Questa è un’altra fase estremamente importante. Tracker dà anche la possibilità di tracciare in automatico il movimento della palla, ma dalle prove effettuate sembra che la traccia manuale, fotogramma per fotogramma, porti a dei risultati più precisi, perché durante il tracciamento automatico il cursore tende a posizionarsi in puti diversi della palla. 
   Sarebbe utile avere una zona di riferimento sulla palla (ad esempio una zona diversamente colorata) per poter posizionare il puntatore su di essa in ogni fotogramma.

I risultati che si ottengono al termine di queste operazioni sono visualizzati nelle immagini che seguono. 

In figura 1 osserviamo il percorso della palla in un primo lancio (Caso 1) (ogni quadratino rosso indica la posizione occupata dalla palla all’istante t (espresso in secondi). Le coordinate x e y (espresse in cm)  di ogni posizione tracciata sono quelle riportate nella tabella della figura.

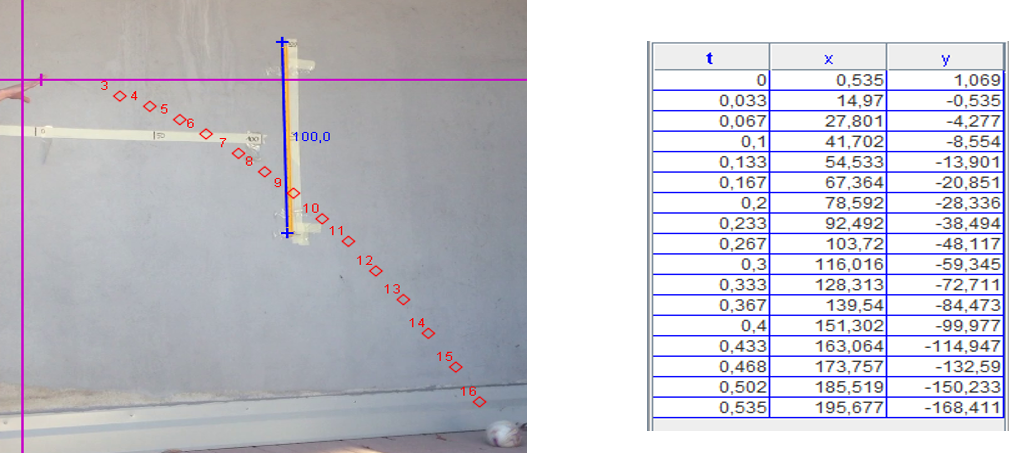
In figura 2 osserviamo il percorso della palla in un secondo lancio (caso 2); le coordinate x e y (espresse in cm)  di ogni posizione tracciata sono riportate nella tabella della figura.

Il software, utilizzando i dati raccolti nella tabella, traccia i grafici  y=y(t) e x=x(t); figura 3 mostra i grafici nel caso 1.

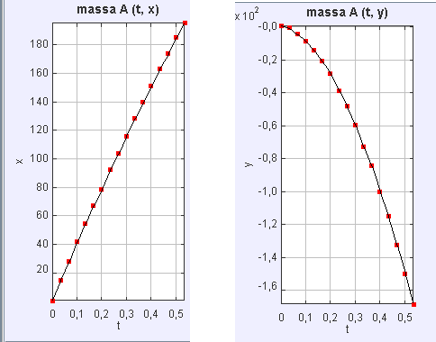
Il fit delle due curve fornisce i seguenti risultati:

Figura 4 mostra i grafici nel caso 2.

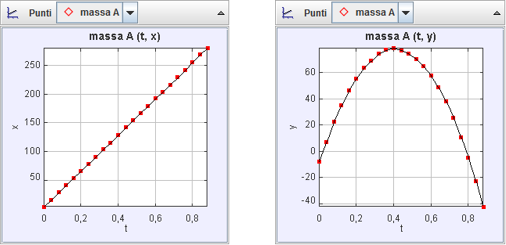
In questo caso il fit delle due curve fornisce i seguenti risultati:

I grafici  mostrano chiaramente che  la palla si muove di moto uniformemente accelerato lungo la direzione verticale e di moto rettilineo uniforme lungo la direzione orizzontale.

A questo punto si passa all’analisi dei dati. Si può decidere di continuare ad utilizzare Tracker oppure di esportare i dati relativi al tempo e alle posizioni (dal Menù File si seleziona la voce Esporta file di dati) e di  analizzarli con altri software, ad esempio con Excel.

Nel nostro caso abbiamo utilizzato esclusivamente Tracker.  Mediante il fit quadratico dei dati sperimentali abbiamo trovato l’equazione e il grafico della traiettoria seguita dalla palla. Figura 5 e figura 6 riportano i risultati ottenuti nei due casi.

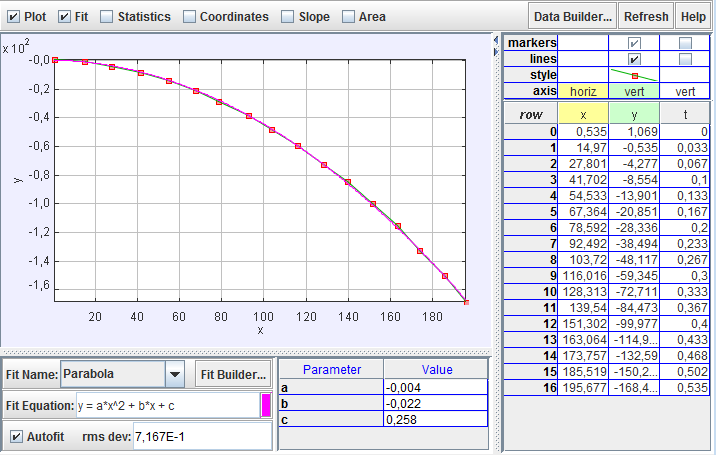
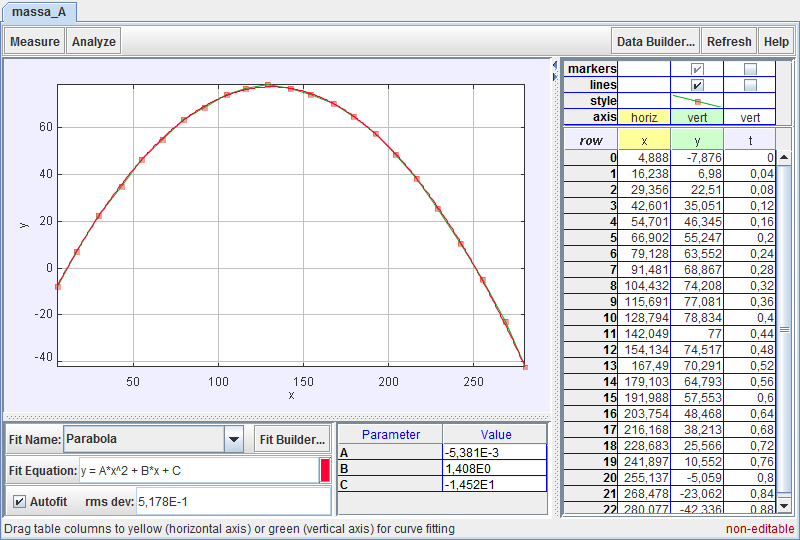
Riportiamo per comodità le equazioni generali del moto parabolico e, a fianco, quelle ottenute con Tracker  in  una tabella:

Dai coefficienti delle equazioni si ricavano  i valori di \(v_{0x}\ e\ v_{0y}\) (in m/s) e il valore dell’accelerazione di gravità \(g\) (in m/s²) (tabella 2).

Il confronto del valore di \(g = 10,6\ m/s^2\) con il  valore atteso \(9,81 m/s^2\), porta a concludere che \(g\) è stata stimata con un errore pari all’8% in entrambi i casi.

QUARTA FASE

I risultati ottenuti sono stati oggetto di discussione durante un’ora di lezione a scuola.

Tutti hanno trovato nelle leggi orarie e nelle traiettorie una conferma di quanto studiato a livello teorico.

L’errore nel calcolo di \(g\) varia però  tra  il 4 e il 10%. Gli studenti si sono chiesti quali possono essere i motivi di queste discrepanze dal momento che tutti hanno avuto a disposizione lo stesso filmato.

Dalla discussione, che ha portato al confronto dei percorsi tracciati e delle tabelle di dati raccolti, si è giunti alla conclusione che la fase che determina risultati diversi  è quella in cui si traccia il percorso della palla. Tale fase, per tutti, è risultata la più delicata.
Abbiamo notato che molta attenzione va posta anche nella realizzazione del filmato (vedi osservazioni all’inizio di questo svolgimento). In particolare, nel Caso1,  ci siamo resi conto che, per imprimere alla palla una velocità iniziale perfettamente orizzontale, sarebbe opportuno appoggiarla  su un tavolo prima di darle la spinta iniziale. Questo accorgimento, che non è stato da noi seguito, ha determinato una componente verticale della velocità iniziale diversa da 0 (come si può osservare nelle tabelle precedenti è pari a 0.56 m/s).

Per questo si è pensato che in futuro potrebbe essere utile realizzare più filmati, in modo da scegliere poi quello più adatto ad essere analizzato.

In conclusione ci sembra che  l’attività qui presentata abbia alcuni vantaggi:

1. consente agli studenti di verificare una legge teorica applicandola ad una situazione reale senza grandi difficoltà;
2. si svolge in tempi brevi;
3. non bisogna  affrontare le difficoltà legate alla misura e alla successiva rielaborazione dei dati sperimentali che, di solito, rendono meno coinvolgente e piacevole per gli studenti l’attività di laboratorio.

Si sottolinea infine che il software Tracker può essere utilizzato senza essere esperti nel suo uso. Bastano delle nozioni di base (come è avvenuto per i nostri studenti) per svolgere attività significative.

Note e storia

Note
(1)  software libero (licenza GNU) che può essere scaricato al seguente indirizzo: http://www.cabrillo.edu/~dbrown/tracker/ Costituisce un efficace strumento di analisi dei moti poiché permette di tracciare il moto di un corpo (o del centro di massa di un sistema) e di modellizzare il fenomeno attraverso appropriate equazioni .
Il manuale d’uso è disponibile al seguente indirizzo: http://www.cabrillo.edu/~dbrown/tracker/tracker_help_it.pdf

Cenni Storici
Nel “Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla meccanica e ai moti locali“, Galileo affronta il problema del moto dei proiettili. Prima di lui, si credeva che un corpo lanciato in direzione orizzontale, per esempio un proiettile sparato da un cannone, si muovesse in direzione orizzontale fino a quando non perdeva il suo “impeto”, dopodiché cadeva verso terra, seguendo una traiettoria curvilinea che però non era ancora conosciuta.
La scoperta fatta da Galileo nel 1604 sulla legge di caduta dei gravi fu importante per i suoi successivi studi sul moto dei proiettili. Galileo nel 1608 comprese che i proiettili percorrono una distanza in orizzontale che e’ proporzionale al tempo impiegato per percorrerla e una distanza in verticale che e’ proporzionale al quadrato del tempo impiegato a percorrerla. Riuscì anche a dimostrare il principio di composizione dei movimenti e che la combinazione dei due moti orizzontale e verticale risulta in una traiettoria parabolica.

Bibliografia

• Libro di testo: A.Caforio, A.Ferilli; FISICA! Le regole del gioco – vol. 1; Le Monnier Scuola
• Approfondimento e applet per la simulazione del lancio del proiettile: http://www.ba.infn.it/~palano/lab/book_lab/it/Chap_2/sec_14/index.html
• Riferimenti storici: Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze, Leida 1639.

Autori

Brambilla Alessandra 
Celora Marina 

Specifiche esperimento Materia Fisica Classi a cui è rivolto 2° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano Materiale specifico Asta graduata o righello, pallina di vetro, software Tracker Durata esperimento in classe 3 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone Sì Parole chiave Meccanica Dinamica del punto materiale Moto uniformemente accelerato Moto di un grave