Riassunto / Abstract

Si propone di ricavare il valore corrispondente al \(\pi\) da misure dirette di lunghezze (diametri e circonferenze)  e di aree. L’ esperienza costituisce un primo approccio all’insegnamento della Fisica sperimentale e al trattamento dell’incertezza delle misure.  Non necessita di strumentazione sofisticata, né di particolari prerequisiti in termini di conoscenze e abilità, è adatta a qualunque classe prima.

Scheda sintetica delle attività

L’esperienza si compone di due parti indipendenti l’una dall’altra.

Parte 1: Relazione tra la lunghezza di una circonferenza e il suo diametro:

• si misura il diametro e la circonferenza delle sezioni circolari di diversi oggetti;
• si verifica che esiste una relazione di proporzionalità diretta tra la lunghezza della circonferenza e quella del diametro corrispondente;
• si calcola la costante di proporzionalità deducendo il valore di \(\pi\) .

Parte 2: Rapporto tra l’area di un cerchio e l’area del quadrato ad esso circoscritto

• si misura direttamente l’area di un cerchio in termini di numero di quadretti contenuti in esso, utilizzando un foglio a quadretti;
• si calcola il rapporto tra l’area del cerchio e l’area del quadrato ad esso circoscritto poi da questo rapporto si deduce il valore di Pi-greco;
• Si ripete l’intera procedura su cerchi di dimensione maggiore, cioè si diminuisce il rapporto tra l’area del singolo quadretto e quella del cerchio: si analizza l’influenza di ciò sull’incertezza della misura delle aree e sul valore di \(\pi\) ricavato.

Risorse necessarie

• Alcuni oggetti con sezione esterna circolare (diametro variabile da 1 a 15 cm circa);
• foglio grande (almeno formato A3) di carta da riciclo;
• riga da disegno (portata 50 cm, sensibilità 1 mm);
• foglio elettronico;
• foglio protocollo a quadretti;
• compasso;
• penne colorate.

Prerequisiti necessari

L’esperienza non necessita di alcuna competenza teorico-pratica come prerequisito

Obiettivi di apprendimento

• Nozioni sugli errori di misura;
• significato di valore medio, semidispersione massima e deviazione standard;
• calcolo dell’errore sulla media;
• rappresentazione delle misure su grafici cartesiani;
• analisi grafica di una proporzionalità diretta;
• determinazione della costante di proporzionalità.

Dotazioni di sicurezza

Nessuna

Svolgimento

Introduzione

L’esperienza è adatta a qualunque classe prima. Proposta all’inizio dell’anno scolastico può essere utilizzata per introdurre i concetti base di teoria della misura quali il valore medio, l’errore massimo, l’errore statistico, l’incertezza, collegandoli subito a misure reali.

Disponendo di computer, l’esperienza fornisce lo spunto per presentare il foglio elettronico e per insegnare come disegnare tabelle per la raccolta e l’elaborazione dei dati sperimentali, introdurre formule di calcolo, costruire grafici cartesiani rappresentando valori medi e relative incertezze. Se non si dispone di computer si può comunque utilizzare una calcolatrice e la carta millimetrata.

L’esperienza si è sempre rivelata molto coinvolgete per i ragazzi sia nella parte pratica delle misurazioni che in quella più teorica dell’elaborazione grafico-matematica. Le conclusioni spesso sorprendono lo studente abituato a collegare il numero Pi-greco solo a formule già note di geometria, senza sapere che può essere derivato dall’analisi di semplici misure di lunghezza effettuate all’interno della disciplina Fisica.

Relazione tra la lunghezza di una circonferenza ed il suo diametro

• Si scelgono alcuni oggetti di uso comune che abbiano una sezione esterna circolare. Se si dispone di un calibro è possibile misurare anche sezioni interne. Nell’esempio riportato sono stati utilizzati un rotolino di scotch, un cilindro graduato, un becher grande, una bomboletta spray, un barattolo e una colla stic.

• Ogni ragazzo misura la lunghezza della circonferenza e del diametro di una sezione scelta per ciascun oggetto.
  Per la misura del diametro si utilizza un semplice righello oppure una riga da disegno. Per sezioni situate all’interno dell’oggetto si può utilizzare un calibro limitando la lettura alla sola scala dei millimetri.
  Per la misura della circonferenza si utilizzano delle striscette di carta alte circa 1 cm ritagliate da un foglio formato A3: si fanno ben aderire al contorno considerato, si prende un segno sul punto di sovrapposizione; si distende poi la striscetta e si misura la lunghezza interessata con una riga.

Si compila una tabella per ogni oggetto che raccoglie le misure di tutti i ragazzi

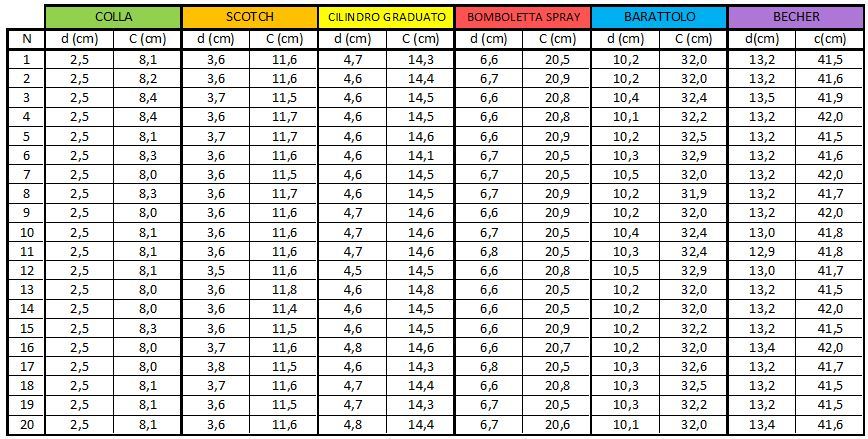
• Con l’utilizzo di un foglio elettronico si determina il valore medio e l’incertezza delle misure di circonferenza e diametro effettuate. Essendo la prima volta che gli studenti si cimentano in misurazioni e trattamento dati, si è deciso di seguire una procedura semplificata nella determinazione dell’errore, considerando quale errore sul valore medio la deviazione standard dei valori misurati.
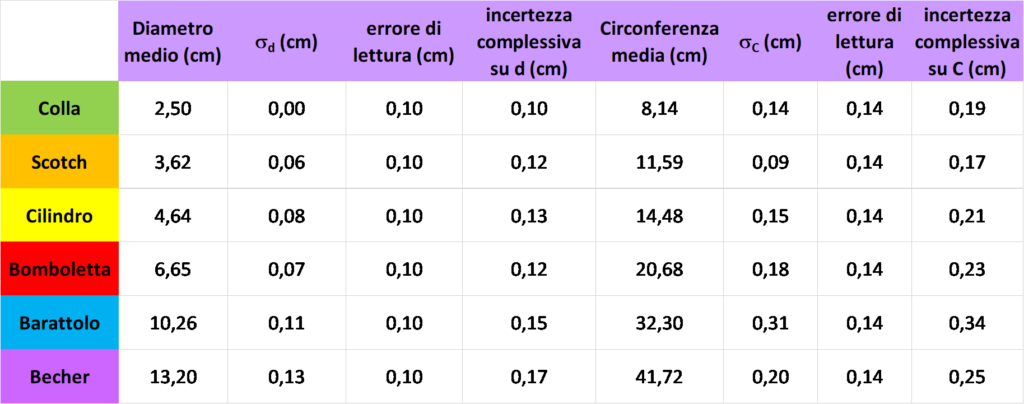
• Come errore di lettura, dopo averne ampiamente discusso con la classe, si è scelta la sensibilità dello strumento utilizzato (0,1 cm) per le misure di diametro mentre per le misure di circonferenza un valore maggiore,  considerato il doppio intervento con la striscetta di carta (accostamento all’oggetto + accostamento alla riga) necessario per poter eseguire la misura, ottenuto mediante somma in quadratura dei due errori di sensibilità (0,1 cm) su ciascuna operazione
• L’incertezza complessiva è stata determinata mediante la somma in quadratura della incertezza sulla media e di quella di lettura.

• La figura seguente mostra il grafico dell’andamento della lunghezza della circonferenza al variare del diametro

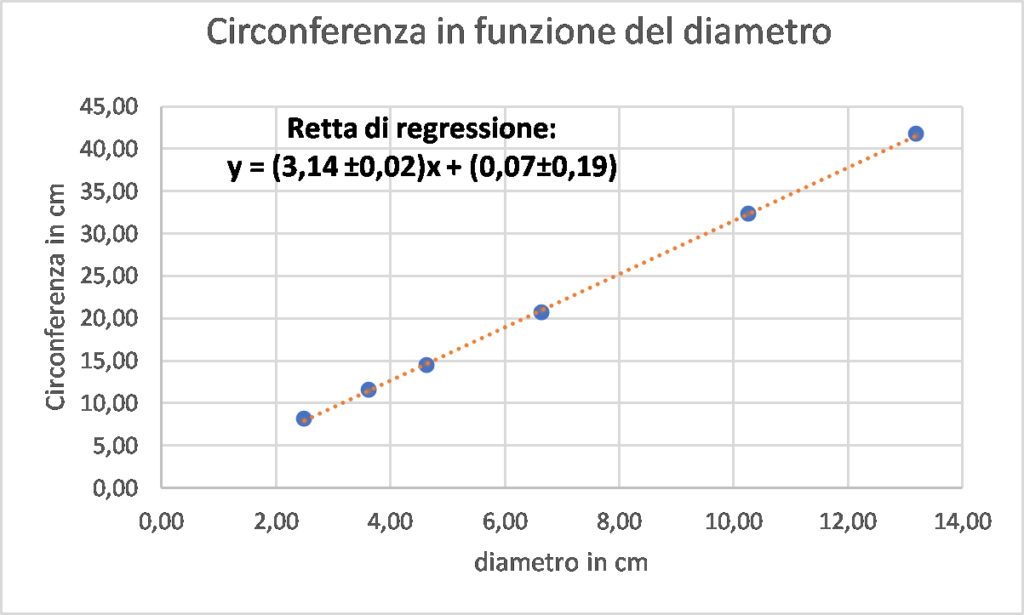
• L’osservazione di questo primo grafico porta alla verifica della relazione di proporzionalità diretta tra la lunghezza della circonferenza e quella del suo diametro. Infatti esiste almeno una retta passante per l’origine e per tutti i punti sperimentali rappresentati dalle corrispondenti superfici d’indeterminazione.
  L’elaborazione fatta con EXCEL permette di evidenziare la linea che meglio approssima l’andamento dei dati rappresentati, fornendone anche l’equazione. Il coefficiente angolare di questa retta rappresenta la costante di proporzionalità e quindi il valore di \(\pi\) cercato, che risuta quindi essere

• Per associare al valore trovato un margine d’incertezza che tenga conto anche delle indeterminazioni sui singoli valori dei diametri e delle circonferenze, si tracciano sul grafico le rette di massima minima pendenza passanti per l’origine e per tutti i punti sperimentali:

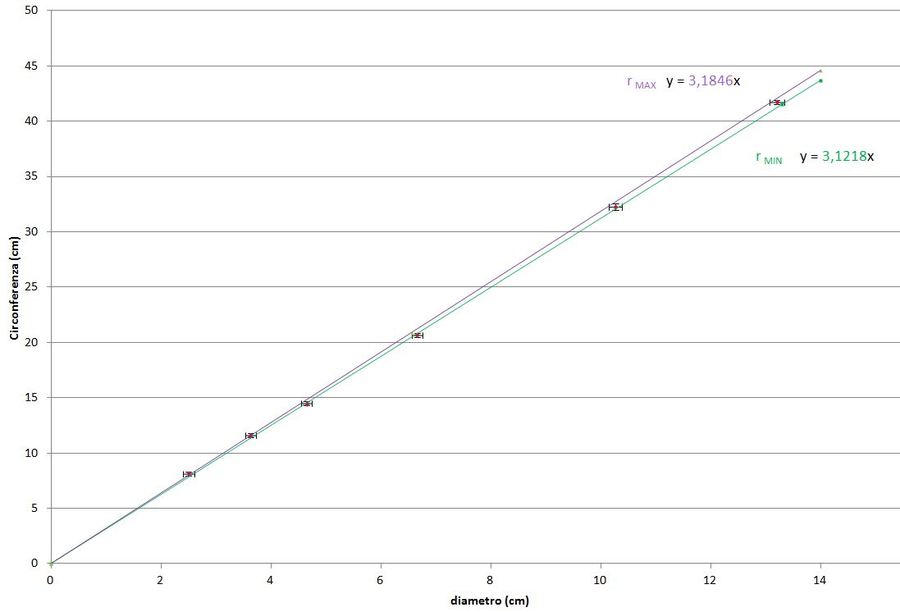
Da questo grafico si ricavano i valori massimo e minimo per \(\pi\) :

Otteniamo infine per  il valore medio e la semidispersione:

Il risultato finale si può scrivere nella forma

Il risultato trovato presenta un buon grado di precisione in quanto l’errore relativo percentuale è di circa l’1%:

Seconda parte: Rapporto tra l’area di un cerchio e l’area del quadrato ad esso circoscritto

• Su un foglio protocollo a quadretti piccoli (lato quadretto 4mm) si disegna con il compasso una circonferenza di raggio 10 quadretti e il quadrato ad essa circoscritto.
• Si contano i quadretti che si trovano completamente all’interno del cerchio (verdi in figura 5) e si indica questo numero con \(A_{min}\) .

.Si contano i quadretti che si trovano completamente all’interno del cerchio (verdi in figura 5) e quelli che non sono completamente esterni al cerchio (gialli in figura 5) e si indica questo numero con \(A_{max}\).

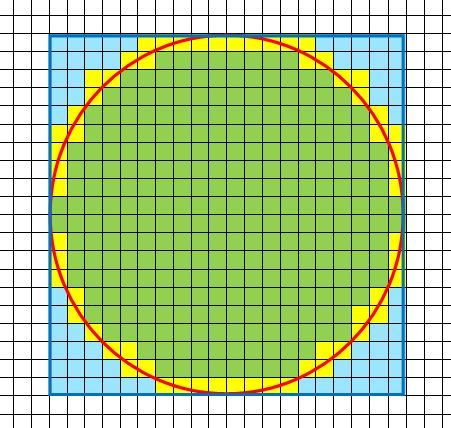
Con riferimento alla figura, si trova:  \(A_{min} = 277 q\)  e \(A_{max} = 338 q\)

L’ area del quadrato circoscritto è : \(A_{quadrato} =  400 q\)

• Utilizzando note formule di geometria, si osserva che:

 per cui:

• Si determina il valore di \(\pi\) inserendo i valori misurati nella relazione precedente; si ottiene così un valore massimo per  \(\pi\)  in corrispondenza di \(A_{max}\) e un valore minimo in corrispondenza di \(A_{min}\).. Risulta: 

Assumiamo come errore la semidispersione \(\Delta\) dei valori trovati: 

Il risultato della misura è quindi:

La procedura utilizzata in questa seconda parte  per arrivare al valore di \(\pi\) è molto semplice ma il risultato trovato è piuttosto scadente, infatti l’errore relativo percentuale \(\epsilon _{\%}\) è circa il 10%:

Per migliorare il risultato occorre aumentare la sensibilità del metodo, aumentando il rapporto tra area da misurare e l’unità di misura scelta, cioè la dimensione del quadratino;  si potrebbe sostituire il foglio a quadretti con carta millimetrata, utilizzando così uno strumento 16 volte più sensibile.
Purtroppo l’individuazione delle aree da misurare e il conteggio dei quadratini in questo caso diventa davvero complesso. Per questo è consigliabile aumentare l’area del cerchio piuttosto che diminuire quella del quadretto.

• Si ripetono per questo tutti i passi precedenti partendo da una circonferenza avente raggio di 15 quadretti prima e 20 quadretti poi.

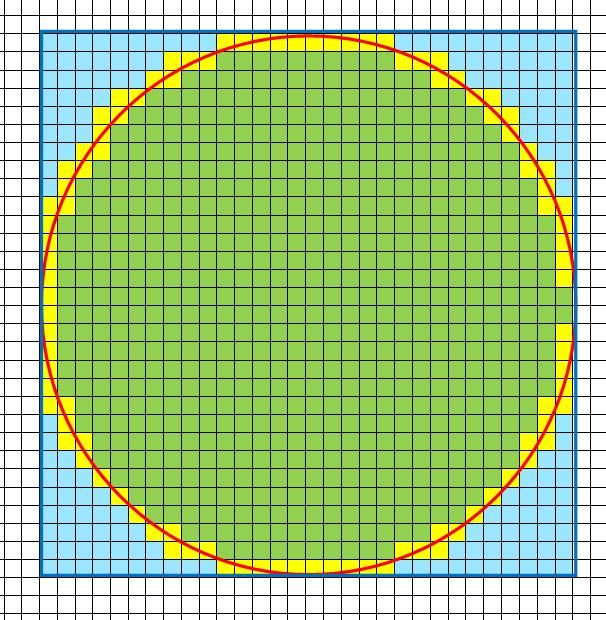
Con riferimento alla figura, si trova: \(A_{min} = 649 q\) e \(A_{max} = 748 q\)

L’ area del quadrato circoscritto è : \(A_{quadrato} =  900 q\)

Il risultato della misura è quindi:

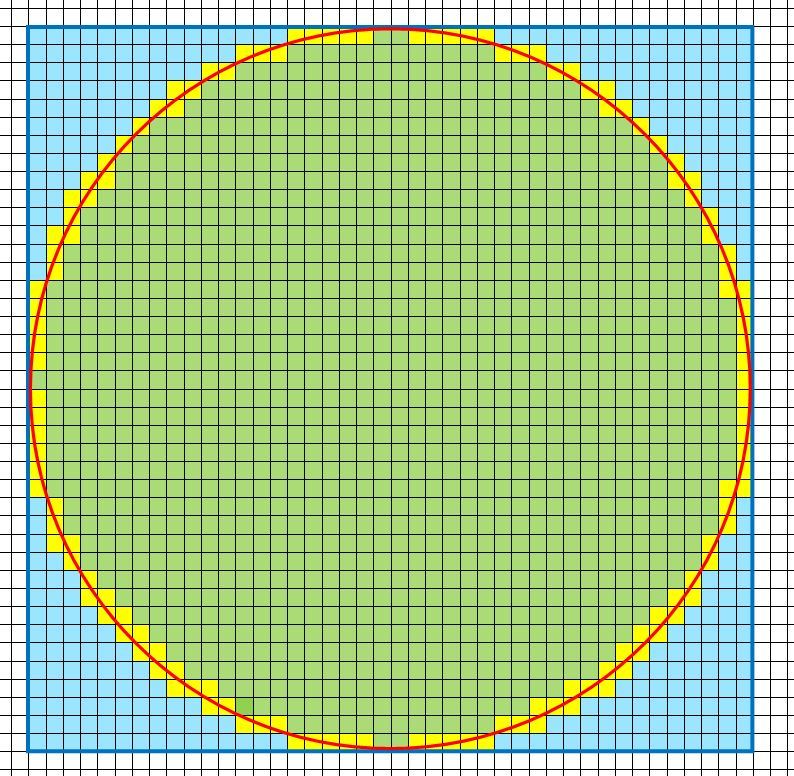
Con riferimento alla figura, si trova: \(A_{min} = 1234q\) e \(A_{max} = 1367q\)

L’ area del quadrato circoscritto è : \(A_{quadrato} = 1600q \)

Il risultato della misura è quindi:

Notare come rispetto alla prima costruzione grafica l’errore relativo percentuale nell’ultimo caso si è all’incirca dimezzato.

La conclusione dell’intera esperienza è affidata al confronto dei risultati ottenuti con i due diversi metodi seguiti e alla discussione sull’opportunità o meno di seguire l’uno o l’altro.

Note e storia

Mentre la classe portava avanti questo lavoro, l’insegnante di matematica ha incaricato gli studenti di fare una ricerca sulla storia del numero PI-GRECO. I risultati di questa ricerca sono stati raccolti nella presentazione power point allegata.

Autori

De Paolis Paola 

Schede / Allegati

• Breve storia del PI-GRECO

Specifiche esperimento Materia Fisica Classi a cui è rivolto 1° biennio Tipologia di laboratorio Povero Reperibilità del materiale Uso quotidiano Materiale specifico Oggetti con sezione esterna circolare, foglio grande, riga da disegno, foglio protocollo a quadretti, compasso, penne colorate Durata esperimento in classe 6 h Capacità di bricolage/assemblaggio No Necessità lavorazioni meccaniche/elettroniche No Necessità PC per acqusizione/analisi dati Sì Necessità di uno smartphone No Parole chiave Metodo sperimentale Teoria della misura Misure indirette Propagazione degli errori