11) Camera stenopeica solare

geografia astronomica luce ottica geometrica

In questo esperimento si costruisce una camera stenopeica per osservare il Sole e calcolarne il diametro.

Lo schema di un prisma bianco, contenuta in un esagono verde acqua

Scheda esperimento

Classi 1° biennio
Tipologia Povero
Durata 2 h
Consulta la legenda delle icone.

Scheda sintetica delle attività

Si realizza la camera stenopeica, utilizzando un tubo di cartone di 1 m di lunghezza rivestito internamente dal cartoncino nero o verniciato in nero al fine di ridurre la diffusione della luce sulle pareti interne.
Le due superfici agli estremi del tubo sono chiuse rispettivamente con un foglio di carta stagnola nel quale è stato praticato un foro di spillo e con un foglio di carta traslucida, fissati con elastici o con nastro adesivo.
Occorre rivolgere la superficie con il foro dello strumento verso il Sole fino a che non appare l’immagine di quest’ultimo sulla superficie opposta. Si posiziona lo strumento con il foro verso il Sole e si osserva la sua immagine, disegnandone il contorno.
Si misura il diametro dell’immagine; poi, nota la distanza Terra-Sole e usando la similitudine dei triangoli, si calcola il diametro del Sole.

Risorse necessarie

  • Un tubo di cartone o una scatola;
  • foglio di alluminio;
  • nastro adesivo e/o elastici;
  • tempera o vernice acrilica spray nera opaca o cartoncino nero;
  • carta translucida e.g. carta da forno o carta lucida da disegnatore;
  • forbici e altri utensili utili.

Prerequisiti necessari

  • Conoscere e saper applicare ii criteri di similitudine dei triangoli.

Obiettivi di apprendimento

  • Imparare a osservare un fenomeno comune come la propagazione della luce
  • Imparare a proporre ipotesi e modelli esplicativi
  • Saper verificare le ipotesi fatte
  • Saper utilizzare la triangolazione per misure di distanza
  • Essere in grado di utilizzare un fenomeno comune per effettuare una misura

Dotazioni di sicurezza

Nessuna in particolare; raccomandare agli studenti di non osservare la luce diretta del Sole.

Svolgimento

Una camera stenopeica è un semplice dispositivo ottico (detto anche camera oscura) costituito da una scatola chiusa in cui su una parete è praticato un piccolo foro (figura 1).

Sulla faccia opposta, grazie alla propagazione rettilinea della luce, si forma un’immagine che può essere osservata ad occhio nudo o registrata attraverso una carta fotosensibile o un rivelatore.

Questo strumento può essere utilizzato per osservare il Sole ed effettuare alcune istruttive esperienze didattiche.

A sinistra dell'immagine c'è un albero, a destra una scatola con un foro, nella direzione dell'albero, e sul cui fondo è rappresentata l'immagine dell'albero rovesciata, con la chioma in basso e le radici in alto. Le estremità tra l'albero "reale" e quello "proiettato" sul fondo della scatola sono connesse da due rette in rosso che passano per il foro nella scatola.
Figura 1:schema di funzionamento della camera stenopeica

Costruzione e uso dello strumento

  • Lo strumento è realizzato con un tubo di cartone di 1 m di lunghezza rivestito internamente dal cartoncino nero o verniciato in nero al fine di ridurre la diffusione della luce sulle pareti interne. Colorare di nero o rivestire con cartoncino nero l’interno del tubo (o della scatola) per ridurre la diffusione della luce che penetra all’interno del tubo attraverso il foro stenopeico.
  • Le due superfici agli estremi del tubo sono chiuse rispettivamente con un foglio di carta stagnola nel quale è stato praticato un foro di spillo (figura 2) e con un foglio di carta traslucida, fissati con elastici o con nastro adesivo (figura 3 e 4).
  • La luminosità  e la risoluzione dell’immagine dipendono dalla dimensione del foro: aumentandole aumenta la luminosità, ma peggiora la risoluzione.
  • La dimensione dell’immagine non dipende dalla dimensione del foro ne dalla forma: un foro triangolare funziona bene come quello tondo.
  • L’immagine ottenuta con questo strumento non presenta aberrazioni.
un'estremità del tubo di cartone, coperta con un foglio di alluminio in cui è stato praticato un piccolo foro
Figura 2: un’estremità del tubo di cartone, coperta con un foglio di alluminio in cui è stato praticato un piccolo foro
l'estremità del tubo di cartone su cui è stato posto un foglio di carta traslucida, fissata con un elastico
Figura 3: un’estremità del tubo di cartone, coperta con il foglio di carta traslucida
tubo di cartone della lunghezza di circa un metro con le estremità sigillate
Figura 4: tubo stenopeico

Prime osservazioni

Gli studenti posizionano lo strumento verso il Sole, osservano la sua immagine e ne disegnano il contorno. 
Si può verificare che:

  • la dimensione dell’immagine non dipende dalla dimensione del foro (per fori piccoli);
  • la luminosità dell’immagine dipende dalla dimensione del foro;
  • la dimensione dell’immagine non dipende dalla forma del foro;
  • la risoluzione del bordo dipende dalla dimensione del foro.
osservazione del Sole: il tubo è tenuto da due mani e rivolto nella direzione del Sole; si visualizza sulla carta traslucida un piccolo dischetto di luce
Figura 5: osservazione del Sole
sulla carta traslucida si visualizza un dischetto di luce, il cui diametro è evidenziato da una freccia rossa
Figura 6: l’immagine osservata, di cui si può misurare il diametro

Come passare dall’osservazione all’acquisizione dei dati e alla loro interpretazione? Come stimolare gli studenti a formulare ipotesi e a verificarle?

Attraverso un questionario strutturato in quesiti e in richieste operative, gli studenti riflettono, si pongono domande, mobilitano conoscenze e abilità già in loro possesso, formulano ipotesi, propongono soluzioni.

Possibili cause di errore

Più il tubo è lungo più si possono presentare problemi di allineamento.  Fare attenzione a tenere ben fermo il tubo durante la misura.  Si consiglia di fotografare l’immagine dopo aver incollato un pezzo di carta millimetrata al nostro schermo  (come illustrato in figura 7) e poi stimare la dimensione del diametro dalla fotografia.

Per aumentare la luminosità dell’immagine che si forma si può aumentare la dimensione del foro, ma attenzione perché la zona di penombra intorno all’immagine del disco solare aumenta con la dimensione del foro, quindi il bordo potrebbe risultare poco netto e causare errori nella misura del diametro dell’immagine.

confrontare l'immagine osservata con la carta millimetrata, apponendola sulla parte superiore del fondo del tubo coperto di carta traslucida, per misurare il diametro
Figura 7: confrontare l’immagine con la carta millimetrata per misurare il diametro

Questionario

  • Se dirigi la superficie forata del tubo verso il Sole, cosa noti all’altra estremità?
  • Fai un disegno che riproduca la situazione osservata.
  • Se raddoppio la lunghezza del tubo, come pensi si modifichi l’immagine del Sole?
  • Se aumento il diametro del foro, che succede all’immagine del Sole? Perché?
  • Come pensi che si formi l’immagine del Sole sulla superficie di carta traslucida?
  • Guarda la figura e rispondi:
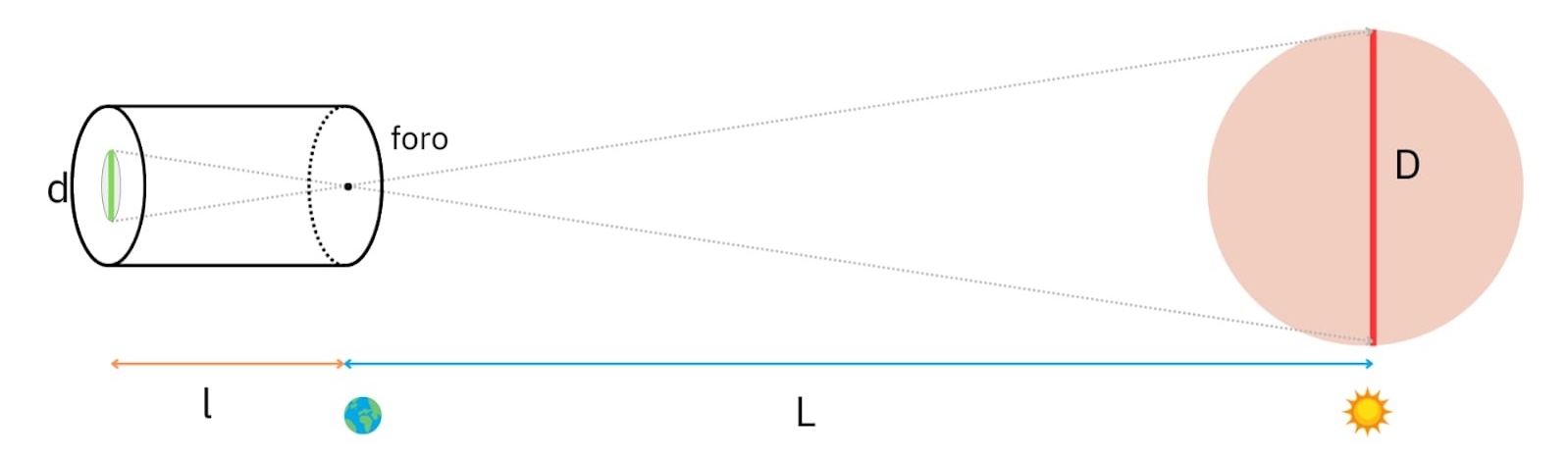
schema geometrico del cammino della luce nella camera stenopeica
Fig. 8: schema geometrico del cammino della luce nella camera stenopeica
  • Come sono tra loro i triangoli che hanno per basi rispettivamente il diametro del Sole e quello dell’Immagine? Perché?
  • Che relazione esiste tra le distanze L e l con i diametri D e d?
  • Immaginando di conoscere la distanza media Terra-Sole \(\left( L= 149,6 \cdot 10^6\ km \right)\) come posso calcolare D?

Misura del diametro solare

  • Si rivolge la superficie con il foro dello strumento verso il Sole fino a che non appare l’immagine di quest’ultimo sulla superficie opposta.
  • Si misura il diametro d dell’immagine.

Per la similitudine dei triangoli abbiamo (figura 8):

\[d\ :\ l\  =\  D\  :\  L\  \longrightarrow D =\frac{L}{l} \cdot d\]

L’errore relativo su D è dato da:

\[\frac{\sigma _D}{D} = \sqrt{  \left( \frac{\sigma_d}{d}\right)^2  +  \left( \frac{\sigma_L}{L}\right)^2 +  \left( \frac{\sigma_l}{l}\right)^2}\]
Esempio

L’immagine di figura 7 è stata ottenuta con un tubo di lunghezza:

\[l = 1.100 \pm 0.003\ m\]

Il diametro misurato dell’immagine d è pari a:

\[d = 1.00 \pm 0.05\ cm\]

La distanza media Terra-Sole, la cosiddetta unità astronomica (u.a.), è pari a:

\[L = 149.6 \cdot 10^6\ km\]

Da questi dati otteniamo:

\[D_{Sole} = \left(1.36 \pm 0.07 \right)\ 10^6\ km\]

Tale valore appare veramente buono se confrontato con il valore comunemente accettato per il diametro solare

\[D=1,392 \cdot 10^6\ km\]

L’errore del 5% è principalmente dovuto all’errore nella misura del diametro dell’immagine.

Ulteriori attività

Variazione di distanza Terra-Sole: si può discutere la possibilità di osservare la variazione di distanza Terra-Sole lungo l’orbita. Noto il diametro solare si può determinare la distanza Terra-Sole in diversi momenti dell’anno per cercare di apprezzare la differenza tra distanza all’Afelio e al Perielio. 
La distanza Terra-Sole varia tra \(147.3 \cdot 10^6\ km\) (Perielio) e \(152.1 \cdot  10^6\  km\) (Afelio) con una differenza del 7% . Con lo strumento usato tale differenza è confrontabile con l’errore di misura. 
Un modo di ridurre l’incertezza può essere quello di utilizzare un tubo più lungo (es. un tubo di grondaia) di almeno 3 m. Anche se leggermente più difficile da allineare permette di ottenere un’immagine di almeno 3 cm di diametro. L’incertezza rimane dell’ordine di 1 mm quindi circa metà rispetto all’effetto che si vuole osservare.

Macchie solari e transiti planetari: si può realizzare una camera stenopeica oscurando una finestra con un cartoncino in cui sia praticato un foro. Osservando le immagini del foro ad almeno 5-6 metri di distanza su uno schermo in una stanza buia è possibile evidenziare gli effetti delle macchie solari o il transito di pianeti.

Dati utili

Unità di misura di distanze astronomiche

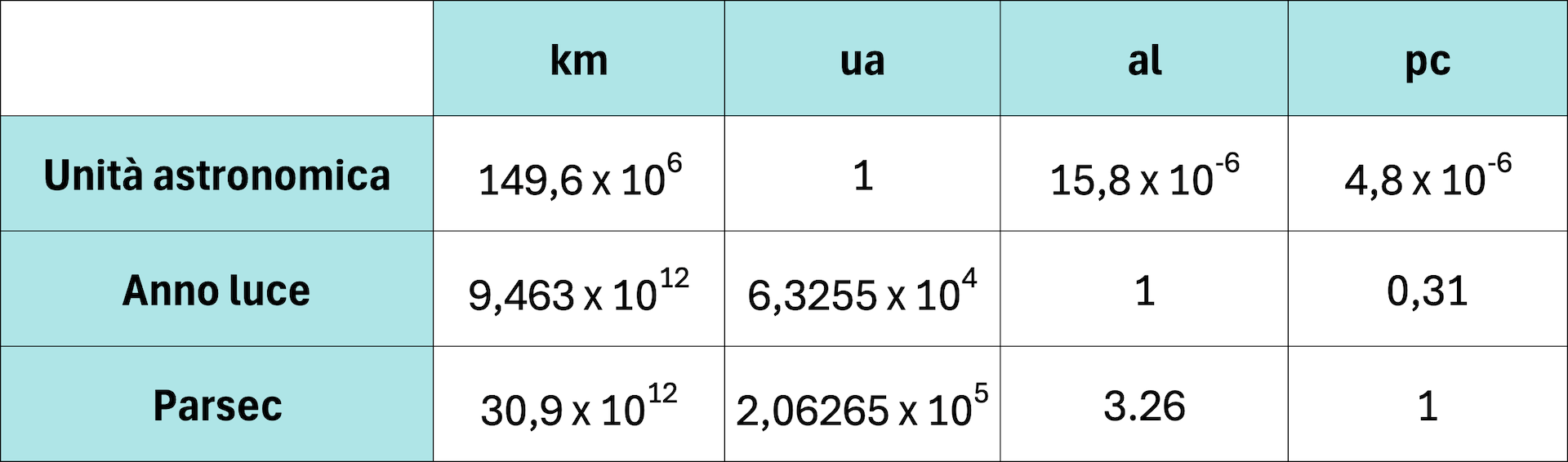
  • Unità astronomica (ua): distanza media Terra-Sole (149 600 000 km)
  • Anno luce (a.l.): distanza percorsa in un anno dalla luce nel vuoto, che viaggia a circa 300 000 km/s (9 463 miliardi di km)
  • Parallasse per secondo (Parsec, pc): distanza dalla Terra di una stella che ha una parallasse di 1 secondo d’arco (30 900 miliardi di km)
fattori di conversione tra di loro delle principali unità di misura utilizzate in astronomia
Tabella 1: fattori di conversione tra di loro delle principali unità di misura utilizzate in astronomia

Note e storia

La scatola stenopeica (dal greco stenos opaios, piccolo foro) è uno strumento elementare per produrre immagini: al posto dell’obiettivo ha un piccolo foro che lascia passare la luce e forma l’immagine sulla parete opposta.

Approfondimenti

Collegamenti interdisciplinari

  • Matematica e Fisica: la geometria euclidea e l’ottica geometrica
  • Arte: i raggi visuali e la tecnica della prospettiva
  • Storia e Filosofia: l’astronomia al tempo dei greci

Bibliografia

Autori

De Angelis Ilaria
Proietti Orietta 
Altamore Aldo 

Schede / Allegati

Torna in alto